计算机视觉 Harris角点检测

一、前言

角点检测在视频分析、计算光流等等技术上都有很大作用。 Harris 检测器是一中比较经典的角点检测器。他是一种具有旋转不变性的检测器，一般使用灰度图片来分析Harris角点。

二、原理

一般来说，一张图中会拥有什么样的信息？

是不是像素的x、y坐标，以及对应的颜色通道？比如RGB……

现在，我们就灰度图像展开讨论。它应该长这样

这里第三维度的信息就是灰度信息。这里就可以很直观地观察梯度信息。

角点是指在某个局部区域中，所有方向上强度变化很大的点。能够作为计算机视觉中重要的特征进行考量。

左图是平坦区域，在所有方向没有明显梯度变化
中图是边缘区域。在某个方向有明显梯度变化
右图是角度边缘，在各个方向梯度值有明显变化

我们知道，只有这个小小的窗口函数在小区域移动时，x 与 y 方向都有明显梯度变化的时候，这个点我们可以视为角点

考虑轴对齐的情况(梯度可以是水平的，也可以是垂直的)

我们可以观察到，只要是在图像的某个局部区域内，x方向与y方向都有明显的数值变化，这个地方的点就可以简单理解为角点。

如果是在边缘的话，就只会在x或y方向上，也就是一个方向上有明显变化

现在，让我们想象一个二维图像I、以及以一个点坐标$x_0,y_0$为中心的$m\times m$大小的一个矩形窗口，就像上图中橙色小窗口那样。

如果我们要评估这个窗口在少量移动过程中，窗口内所发生的强度变化。这种变化可以通过计算平方差和
$$
E(u,v)=\sum_{(x,y)\in Window}w(x,y)[I(x+u,y+u)-I(x,y)]^2（1）
$$

其中：

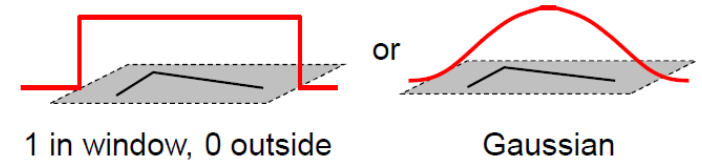
$w(x,y)$是窗口的函数，可以是矩形函数或高斯函数。最简单情形就是窗口内的所有像素所对应的w权重系数均为1。后面讨论的时候有时也会直接取值为1

但有时候，我们会将w(x,y)函数设定为以窗口中心为原点的二元正态分布。参考下面的图：
- 如果窗口中心点是角点时，移动前与移动后，该点的灰度变化应该最为剧烈，所以该点权重系数可以设定大些，表示窗口移动时，该点在灰度变化贡献较大
- 而离窗口中心(角点)较远的点，这些点的灰度变化几近平缓，这些点的权重系数，可以设定小点，以示该点对灰度变化贡献较小，那么我们自然想到使用二元高斯函数来表示窗口函数
$I(x+u,y+u)$是偏移强度。也就是移动前和移动后的灰度差。式子取平方是由于差值有正有负。
$I(x,y)$是原点强度。
整个$E(u,v)$函数是我们需要最大化角点的函数。

窗口的函数，可以是矩形函数或高斯函数

但很快就发现了一个问题：我们相应通过观察u和v来知道这个点是不是角点的话，就得把u和v代回各个这个式子里面，去取像素$I$出来，才能求$E(u,v)$。

我们又需要直接的能够观察u、v和$E(u,v)$之间的关系，每个像素都去代式子来计算显得很不方便。

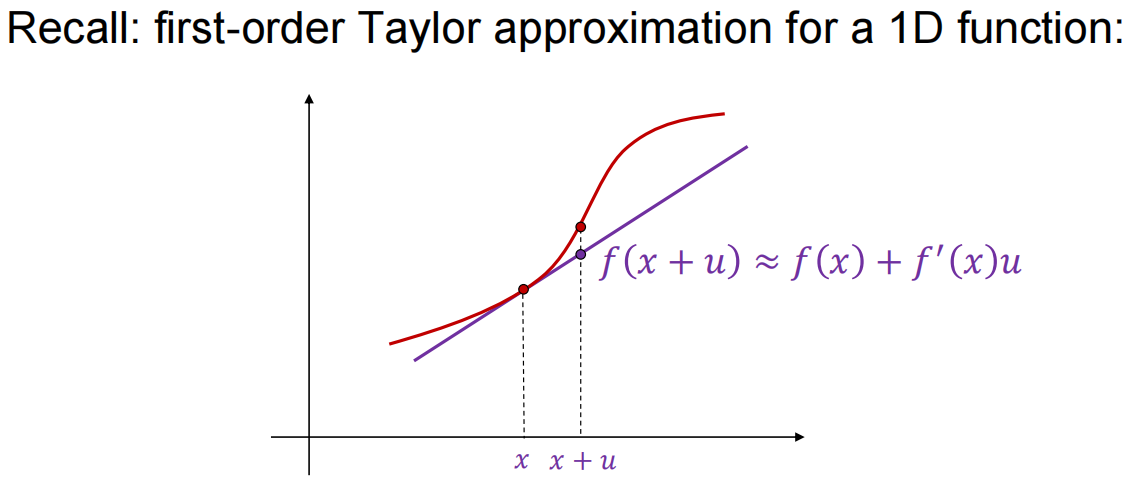
如何直接建立u、v和$E(u,v)$之间的联系？用泰勒展开式。

由于u和v很小，偏移強度$I(x+u,y+u)$可以通过以下一阶泰勒展开来近似：

$$
I(x+u,y+v)\approx I(x,y)+uI_x(x,y)+vI_y(x,y)（2）
$$

一阶泰勒展开

其中$I_x$和$I_y$分别是$I$在x和y方向上的偏导数。我们对式子$I(x+u,y+u)$展开研究。将上述式子（2）代入到式子（1），就可以得到：
$$
E(u,v)=\sum_{(x,y)\in W}w(x,y)[I(x+u,y+u)-I(x,y)]^2\\
\approx\sum_{(x,y)\in W}w(x,y)[I(x,y)+I_xu+I_yv-I(x,y)]^2\\
=\sum_{(x,y)\in W}w(x,y)[I_xu+I_yv]^2\\
=\sum_{(x,y)\in W}w(x,y)[u^2I_x^2+2uvI_xI_y+v^2I_y^2]（3）
$$
式子（3）往矩阵的方向进行化简（这里把$w(x,y)$直接取值为1），可得：
$$
E(u,v)=\sum_{(x,y)\in W}u^2{\color{Red} \Sigma_{x,y}}I_x^2+2uv{\color{Red} \Sigma_{x,y}}I_xI_y+v^2{\color{Red} \Sigma_{x,y}}I_y^2\\=
\begin{bmatrix}
u & v
\end{bmatrix}
\begin{bmatrix}
\sum_{x,y}I_x^2 & \sum_{x,y}I_xI_y \\
\sum_{x,y}I_xI_y & \sum_{x,y}I_y^2
\end{bmatrix}
\begin{bmatrix}
u \\ v
\end{bmatrix}
$$
然后顺理成章的化简为如下矩阵形式：
$$
E(u,v)\approx
\begin{bmatrix}
u & v
\end{bmatrix}
{\color {red}M}
\begin{bmatrix}
u \\ v
\end{bmatrix}
$$
这里面的M称为结构张量，其实就是一个$2\times 2$的根据图像导数计算出来的矩阵。M长这样：
$$
M = \sum_{(x,y)\in W}
\begin{bmatrix}
I_xI_x & I_xI_y \\
I_xI_y & I_yI_y
\end{bmatrix}\\
=\sum_{(x,y)\in W}
\begin{bmatrix}
I_x \\ I_y
\end{bmatrix}
\begin{bmatrix}
I_x & I_y
\end{bmatrix}\\=
\sum\nabla I(\nabla I)^T
$$

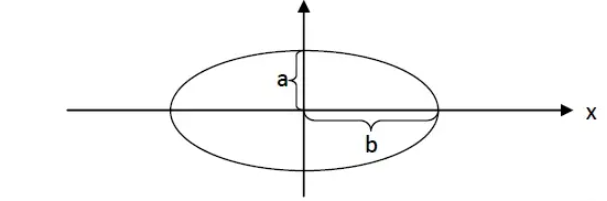
这里中途要杀出一个椭圆函数在矩阵上的表示方式了。

$$
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
$$
这个函数可以改写成：
$$
\frac{x^2}{(a^{-\frac12})^2}+\frac{y^2}{(b^{-\frac12})^2}=1\\
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
\frac{1}{a^2} & 0 \\
0 & \frac{1}{b^2}
\end{bmatrix}
\begin{bmatrix}
x \\ y
\end{bmatrix}=1
$$
而这中间的这个矩阵$\begin{bmatrix}
\frac{1}{a^2} & 0 \\
0 & \frac{1}{b^2}
\end{bmatrix}$，可以获取其中的特征值：
$$
\left\{
\begin{matrix}
\lambda_1=\frac{1}{a^2} \\
\lambda_2=\frac{1}{b^2}
\end{matrix}\right. \\
$$
$$
\left\{
\begin{matrix}
a=\frac{1}{\sqrt{\lambda_1}} \\
b=\frac{1}{\sqrt{\lambda_2}}
\end{matrix}\right.
$$

从上式可以看到，当特征值越大，其对应的椭圆的半轴要越短

关于为什么中途杀出这么个知识点，我只能说：

我们前面研究的M矩阵是：
$$
M = \sum_{(x,y)\in W}
\begin{bmatrix}
I_xI_x & I_xI_y \\
I_xI_y & I_yI_y
\end{bmatrix}
$$
而他是可以被描述为一个带旋转向量R的矩阵M：
$$
M = \sum_{(x,y)\in W}
\begin{bmatrix}
I_xI_x & I_xI_y \\
I_xI_y & I_yI_y
\end{bmatrix}\\=
R^{-1}
\begin{bmatrix}
\lambda_1 & 0\\
0 & \lambda_2
\end{bmatrix}R
$$
这上面，轴长受到$\lambda$影响，方向受到R的影响。

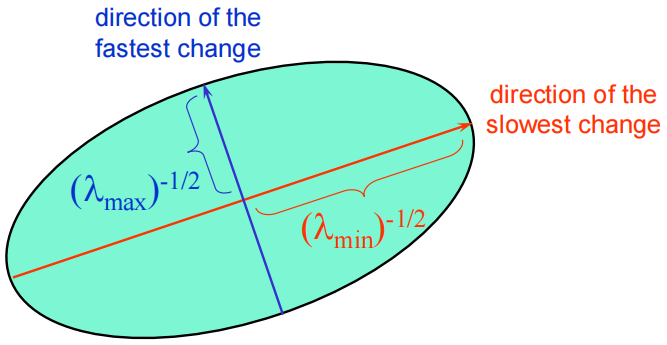
为了更好地分析图像导数数据的主要成分，设当椭圆表达式不存在$I_xI_y$交叉项的时候，此时椭圆的长短轴恰好在x,y方向上

针对这种情况，我们可以把前面那个M矩阵化成：
$$
M=\begin{bmatrix}
\lambda_1 & 0\\
0 & \lambda_2
\end{bmatrix}
$$
由此，我们知道了求得的$E(u,v)$是可以通过椭圆的形式来表达的。

我们使用一张图，使用一个简单的滤波器（比如索贝尔算子）遍历一遍局部区域。

然后将遍历统计到的数据用散点的形式画上去。然后用椭圆形式表示，绘制的图像如下图所示：

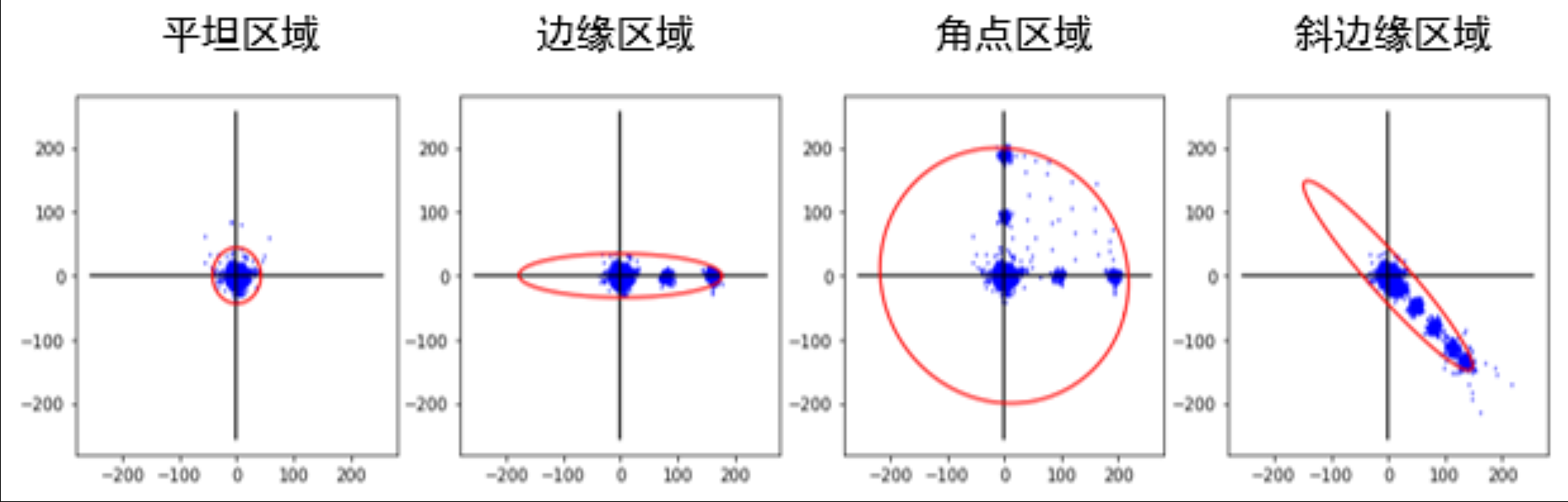
可以观察到，平坦区域的梯度基本没什么变化，边缘区域只有一个方向发生了变化，角点区域则是两个方向。当然两个方向上有变化的也可能是斜边缘区域，这个根据散点分布决定

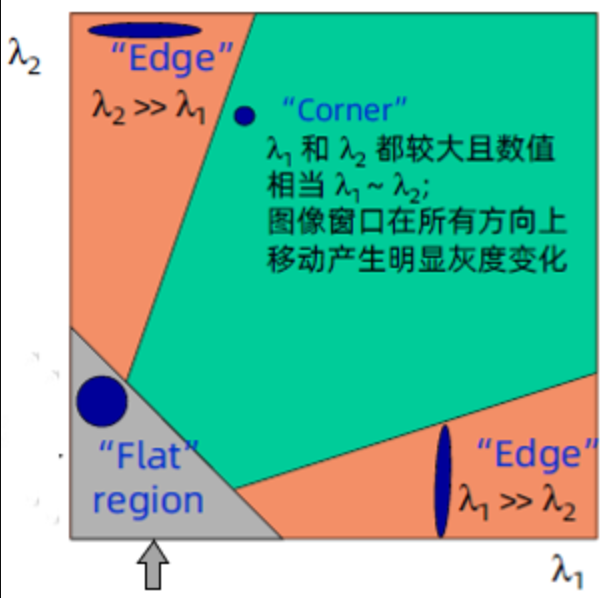
这样一来，我们就可以仅通过矩阵M的特征值，来评估图像是否存在角点

但Harris角点的计算方法甚至不需要用到特征值，只需要计算一个Harris响应值R进行评分
$$
R = \det M-k(\mathbb{trace} M)^2
$$
λ1 和 λ2 是矩阵M的特征值，k是一个经验常数，在范围 (0.04, 0.06) 之间。

这里面计算矩阵M的行列式和迹，代入公式即可。其中：
$$
\det M =\lambda_1\lambda_2\\
\mathbb{trace}=\lambda_1+\lambda_2
$$
有了这个R评价指标，我们就可以将这个窗口所在的区域划分为平面、边缘或角点。
$$
R = \det M-k(\mathbb{trace} M)^2\\
\left\{\begin{matrix}
边缘点 & R<0 \\
平坦点 & |R|\approx 0\\
角点 & R>0
\end{matrix}\right.\\
$$
为了得到最优的角点，我们还可以使用非极大值抑制。

今天这篇不打算详细介绍非极大抑制。其核心思想大致为：抑制非极大值的目标（去冗余），从而搜索出局部极大值的目标（找最优）。

三、总结

哈里斯角点检测一般流程

1、彩色图像转化为灰阶图像
2、计算空间微分（泰勒展开）
3、建构结构张量（Sobel算子）
4、计算哈里斯响应（角点响应）
5、非极大值抑制（筛选点）

四、代码实现

import cv2
import numpy as np

'''
    image: 源图片；
    blocksize：窗口大小；
    ksize：索贝尔梯度计算的Kernel大小；
    k：角点响应R的经验值系数。
'''
def Harris(image, blocksize=2, ksize=3, k=0.04):

    def _Harris(cov,k):
        result = np.zeros([cov.shape[0], cov.shape[1]], dtype=np.float32)
        for i in range(cov.shape[0]):
            for j in range(cov.shape[1]):
                a = cov[i, j, 0]
                b = cov[i, j, 1]
                c = cov[i, j, 2]
                result[i, j] = a * c - b * b - k * (a + c) * (a + c)

        return result

    # Sobel
    sobel_x = cv2.Sobel(image, cv2.CV_32F, 1, 0, ksize=ksize)
    sobel_y = cv2.Sobel(image, cv2.CV_32F, 0, 1, ksize=ksize)

    # 存储R值矩阵
    cov = np.zeros([image.shape[0], image.shape[1], 3], dtype=np.float32)

    # 计算Ix^2,Iy^2与Ix*Iy
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            cov[i,j,0] = sobel_x[i,j] * sobel_x[i,j]
            cov[i,j,1] = sobel_x[i,j] * sobel_y[i,j]
            cov[i,j,2] = sobel_y[i,j] * sobel_y[i,j]

    # 计算梯度和
    cov = cv2.boxFilter(cov, -1, (blocksize, blocksize), normalize=False)

    return _Harris(cov,k)

if __name__ == '__main__':
    imgc = cv2.imread(r"D:\code\opencv_ws\python\mouse.jpg")
    # 将图片转化为灰度图
    img = cv2.resize(imgc,(320,320))
    gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # Harris角点检测
    result = Harris(gray_img, 2, 3, 0.04)
    # 筛选
    pos = cv2.goodFeaturesToTrack(result, 0, 0.01, 10)
    for i in range(len(pos)):
        cv2.circle(img, (int(pos[i][0][0]), int(pos[i][0][1])), 3, [0,0,255], thickness=2)
    cv2.imshow('harris detector',img)
    cv2.waitKey(0)