SLAM 3:李群李代数
一、李群
在第一篇SLAM文章中,介绍了旋转矩阵与变换矩阵, 介绍了若干种描述三维世界刚体运动的方式 。 除了用它们来描述相机的位姿之外,还要对它们进行估计和优化。这个问题可以描述为什么样的相机位姿最符合当前观测数据。而典型的做法就是将其构建成一个优化问题来求解。
其中我们讨论了三维旋转矩阵构成特殊正交群SO(3) ,而变换矩阵构成特殊欧氏群SE(3),我们把它的描述搬过来:
$$
SO(3)=\left \{ R \in \mathbb R ^{3 \times 3} | RR^T=I,det(R)=1\right \}
\\
SE(3)=\left \{
T=
\begin{bmatrix}
R & t\\
0^T & 1
\end{bmatrix}
\in
\mathbb R^{4 \times 4} |
R\in SO(3),t\in \mathbb R^3
\right \}
$$
群的概念为了方便,这里把上一篇对群的介绍也搬到这里来:
群是一种集合加上一种运算的代数结构,如果集合为A,运算为+,那么可以记为群G=(A , +)。群要求这个运算要满足以下几个条件:
封闭性:$\forall a,b \in A,a1 \cdot a2 \in A $
结合律:$\forall a,b,c \in A,(a1 \cdot a2)\cdot a3=a1 \cdot (a2 \cdot a3)$
幺元:$\exists a0 \in A,s.t. \forall a\in A,a_{0}\cdot a=a\cdot a_{0}=a$
逆:$\forall a \in A,\exists a^{-1} \in A, s.t.: a\cdot a^{-1}=a_{0}$
可以巧记为:封结幺逆(凤姐要你)
实在不好理解的话,可以把群类比成一个魔方,魔方的旋转就是运算,得到的运算结果(集合中的元素们)就是旋转魔方后,魔方上面整体的颜色分布。
魔方一共就那些颜色排列组合,把所有魔方颜色分布的排列组合集合起来,就是整个集合,在满足 “旋转” 这个运算的前提下,这些集合就构成群(因为如果你选择把魔方拆开这个运算,那得到的一定是散成一片的方块,该状态就不在上述魔方例子的集合内)
易得,旋转矩阵集合和矩阵乘法构成群,后面要介绍的变换矩阵
SE(n)和矩阵乘法也构成群。正因为如此,才能称他们为旋转矩阵群和变换矩阵群。李群是指具有连续(光滑)性质的群。
像整数群$\left \langle \mathbb Z,+ \right \rangle $就是离散的,并不是李群。
像SO(n),SE(n),在实数空间上是连续的,我们可以稍微想象一下,一个刚体在空间中连续的旋转,所以这种算是李群.需要好好理解。
矩阵常见的群有:
- 一般线性群GL(n):指n×n的可逆矩阵,对矩阵乘法构成群
- 特殊正交群SO(n):就是旋转矩阵群,SO(2)和SO(3)是最常见
- 特殊欧氏群SE(n):n维欧氏变换,SE(2)和SE(3)是最常见
插一句,如果足够细心的话,可以发现旋转矩阵、变换矩阵,他们对加法是不封闭的。换句话说,对任意两个旋转矩阵R、或变换矩阵T进行矩阵意义上的相加,得到的不再是一个旋转矩阵或变换矩阵:
$$
R_1+R_2\notin SO(3) \\
T_1+T_2\notin SE(3)
$$
不过呢,他们在乘法上是封闭的
$$
R_1R_2\in SO(3) \\
T_1T_2\in SE(3)
$$
在SLAM相机姿态估计中,SO(3)与SE(3)是很重要的,所以本系列文章主要还是讨论这两个群。
二、李代数
为了便于理解,我们从SO(3)开始讨论,引出SO(3)的李代数$\mathfrak{so}(3)$
0、矩阵求导
1)标量函数对向量求导
设x为向量,设$x\in \mathbb{R}^m$,是个列向量,那么:
$$
\frac{df}{dx}=\left [ \frac{df}{dx_1} ,\frac{df}{dx_2},\cdots,\frac{df}{dx_m}\right ] \in \mathbb{R}^m
$$
一般称这种$\frac{df}{dx_1}$为梯度或Jacobian
2)向量函数对向量求导
设F(x)为一个向量函数:
$$
F(x)=\left [ f_1(x),f_2(x),\cdots,f_n(x) \right]
$$
其中每一个fn都是一个自变量为向量,取值为标量的函数。
$$
\frac{\partial F }{\partial x^T}=
\begin{bmatrix}
\frac{\partial f_1}{x^T} \\
\vdots \\
\frac{\partial f_n}{x^T}
\end{bmatrix}=
\begin{bmatrix}
\frac{\partial f_1}{x_1} & \frac{\partial f_1}{x_2} & \cdots & \frac{\partial f_1}{x_m}\\
\frac{\partial f_2}{x_1} & \frac{\partial f_2}{x_2} & \cdots & \frac{\partial f_2}{x_m}\\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_n}{x_1} & \frac{\partial f_n}{x_2} & \cdots & \frac{\partial f_n}{x_m}
\end{bmatrix}
\in \mathbb{R}^{n\times m}
$$
也就是写成列向量函数对行向量求导的形式,得到一个n×m的雅可比矩阵。典型的写法如下:
$$
\frac{\partial Ax}{\partial x^T}=A
$$
反之,一个行向量也可以对列向量求导,结果为之前的转置:
$$
\frac{\partial F^T}{\partial x}=\left( \frac{\partial F}{\partial x^T} \right)^T
$$
本系列文章习惯使用列向量函数对行向量求导的形式,不引起歧义的前提下忽略其分母上向量的转置符号。
1、李代数的引出
考虑任意旋转矩阵,我们知道:
$$
RR^T=I
$$
现在,R是某一只相机📷的旋转,他会随着时间变化,而连续的变化。我们声明一个函数R(t),表示相机随着时间的推移而转来转去。
他还是一个旋转矩阵对嘛?我们记为:
$$
R(t)R(t)^T=I
$$
好,接下来在等式两边对时间求导,根据求导法则得:
$$
\dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0
\\
\dot{R}(t)R(t)^T=-\left( R(t)\dot{R}(t)^T \right)^T
$$
由此可以看出,$\dot{R}(t)R(t)^T$是一个反对称矩阵。我们在第一篇介绍叉积的时候,介绍到^符号,它可以把一个矩阵变成反对称矩阵。
那同理,我们就可以拿任意一个反对称矩阵找到其对应的矩阵:
$$
a^{\wedge} = A =
\begin{bmatrix}
0 & -a_{3} & a_{2}\\
a_{3} & 0 & -a_{1}\\
-a_{2} & a_{1} & 0
\end{bmatrix}
;A^{\vee} = a
$$
所以,对于$\dot{R}(t)R(t)^T$这一个反对称矩阵来说,按道理上说是可以找到一个三维向量$\phi(t)\in\mathbb{R}^3$与之相对应:
$$
\dot{R}(t)R(t)^T=\phi(t)^{\wedge}
$$
然后等式两边右乘一个R(t),因为R是正交矩阵:
$$
\dot{R}(t)R(t)^TR(t)=\phi(t)^{\wedge}R(t)\\
\dot{R}(t)=
\begin{bmatrix}
0 & -\phi_{3} & \phi_{2}\\
\phi_{3} & 0 & -\phi_{1}\\
-\phi_{2} & \phi_{1} & 0
\end{bmatrix}
R(t)
\\“(式子一)”
$$
由上可看出,每对旋转矩阵求一次导数,只需要左乘一个$\phi(t)^{\wedge}$即可。
考虑到t0=0时,设旋转矩阵R(0)=I,按照导数定义,可以把R(t)在t=0附近进行一阶泰勒展开:
$$
R(t)\approx R(t_0)+\dot{R}(t_0)(t-t_0)\\
=I+\phi(t_0)^{\wedge}(t)
$$
若求t=t1时的姿态:
$$
R(t_1)=I+\phi(t_0)^{\wedge}(t_1)
$$
此R(t1)代表t0到t1的变换。
可以看到,$\phi$反映了R的导数性质,所以称之为:它在SO(3)原点附近的正切空间(Tangent Space)上。
同时在t0附近,设$\phi$保持为常数$\phi(t_0)=\phi_0$,那根据上面标注的**(式子一)**的公式可得:
$$
\dot{R}(t)R(t)^TR(t)=\phi(t)^{\wedge}R(t)\\
\dot{R}(t)=\phi_0(t)^{\wedge}R(t)\\
$$
上式子是一个关于R的微分方程,且有初始值R(0)=I,解得:
$$
R(t)=\exp(\phi^{\wedge}t)=e^{\phi^{\wedge}t}
$$
上式可以看出:旋转矩阵 R 与反对称矩阵$\phi^{\wedge}t$ ,是通过指数函数 exp联系在一起。
2、李代数的定义
每个李群都有与之对应的李代数
李代数描述了李群的局部性质,是单位元附近的正切空间。一般的定义如下:
李代数由一个集合$\mathbb{V}$,一个数域$\mathbb{F}$,和一个二元运算符$[\otimes]$组成。
如果他们满足以下性质,则称$(\mathbb{V},\mathbb{F},[\otimes ])$为一个李代数,记作$\mathfrak{g} $
封闭性:$\forall X,Y\in\mathbb{V},[X\otimes Y]\in \mathbb{V}$
双线性:对$\forall X,Y,Z\in \mathbb V,z,b\in \mathbb F$,有
$$
[aX+bY \otimes Z]=a[X\otimes Z]+b\left[Y\otimes Z\right]
\\
\left[Z \otimes aX+bY\right]=a[Z\otimes X]+b[Z\otimes Y]
$$自反性:自己与自己运算为0:
$$
\forall X\in\mathbb V,[X\otimes X]=0
$$雅克比等价:
$$
\forall X,Y,Z\in\mathbb V\\
,[X\otimes[Y\otimes Z]]+
[Y\otimes[Z\otimes X]]+
[Z\otimes[X\otimes Y]]=0
$$其中这个二院运算符也称为李括号。相比群中较为简单的二元运算,李括号主要是表达了两者之间的差异。
他不要求结合律,要求的是元素和自己进行李括号运算后的结果为0.
举个栗子🌰:三维向量定义的叉乘运算就是一种李括号,所以$\mathfrak{g}=(\mathbb R^3,\mathbb R,\times) $构成了一个李代数。
3、李代数so(3)
为了方便,so(3)和$\mathfrak{so}(3)$描述的是同个东西
前面提到的那个三维向量$\phi$,事实上是一种李代数。SO(3)对应的李代数是定义在$\mathbb{R}^3$上的向量。每一个$\phi$都可以生成一个反对称矩阵:
$$
\Phi=\phi^{\wedge}=
\begin{bmatrix}
0 & -\phi_{3} & \phi_{2}\\
\phi_{3} & 0 & -\phi_{1}\\
-\phi_{2} & \phi_{1} & 0
\end{bmatrix}
\in\mathbb R^{3\times3}
$$
在此定义下,两个向量Φ1与Φ2,的李括号为:
$$
[\phi_1\otimes\phi_2]=(\phi_1^{\wedge}\phi_2^{\wedge}-\phi_2^{\wedge}\phi_1^{\wedge})^{\vee}
\\=(\Phi_1\Phi_2-\Phi_2\Phi_1)^{\vee}
$$
由于向量$\phi$与反对称矩阵是一一对应的, 因此李代数 so(3) 是三维向量组成的集合,其元素是三维向量或者三维反对称矩阵,相当于旋转向量就是李代数:
$$
\mathfrak{so}(3)=\left\{\phi\in\mathbb R^3,\Phi=\phi^{\wedge}\in\mathbb R^{3\times 3}\right\}
$$
而李代数$\mathfrak{so}(3)$和李群$SO(3)$之间的关系是通过指数映射给定的:
$$
R=\exp(\phi^{\wedge})
$$
关于指数映射后面会有一个汇总,这里还要顺便介绍一下SE(3)对应的李代数se(3)。
4、李代数se(3)
为了方便,se(3)和$\mathfrak{se}(3)$描述的是同个东西
对于SE(3),也有对应的李代数$\mathfrak{se}(3)$,它位于$\mathbb{R}^6$空间中:
$$
\mathfrak{se}(3)=\left\{ \xi =
\begin{bmatrix}
\rho \\
\phi
\end{bmatrix}
\in \mathbb R^6
,\rho\in\mathbb R^3,\phi\in\mathfrak{so}(3),
\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge} & \rho \\
0^T & 0
\end{bmatrix}
\in\mathbb{R}^{4\times 4}
\right\}
$$
变换矩阵的李代数$\mathfrak{se}(3)$的元素$\xi$,是一个六维向量。前三维是平移向量,记作$\rho$,后三维是旋转向量,记作$\phi$,实际上就是李代数$\mathfrak{so}(3)$。
并且,在李代数se(3)中,这里的符号
^不再具有反对称的意思,而是用来表示将一个六维向量转为四维矩阵的意思$\wedge$ 指代 “从向量到矩阵“,$\vee$指代 ”从矩阵到向量“
$$
\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge} & \rho \\
0^T & 0
\end{bmatrix}
$$
所以变换矩阵的李代数可以理解为,由一个平移和一个旋转矩阵李代数 表示的旋转向量构成的向量。
同样的,李代数se(3)也有类似于so(3)李代数的李括号:
$$
\left[ \xi_1 \otimes\xi_2\right]=(\xi_1^{\wedge}\xi_2^{\wedge}-\xi_2^{\wedge}\xi_1^{\wedge})^{\vee}
$$
三、指数与对数映射
1、SO(3)上指数映射
有了李代数和李群的映射关系,我们要如何计算exp(Φ^)?显然他是一个矩阵的指数,在李群李代数中,称为指数映射
任意矩阵的指数映射可以写成一个泰勒展开,但是只有在收敛的情况下才会有结果,其结果还是一个矩阵:
$$
\exp(A)=\sum_{n=0}^{\infty}\frac{1}{n!}A^n\\
=I+A^{\wedge}+\frac{1}{2!}A^2+\frac{1}{3!}A^3+\cdots
$$
同样的,对$\mathfrak{so}(3)$中任意元素$\phi$,也可以定义其指数映射:
$$
\exp(\phi^{\wedge})=\sum^{\infty}_{n=0}\frac{1}{n!}(\phi^{\wedge})\\
=I+\phi^{\wedge}+\frac{1}{2!}(\phi^{\wedge})^2+\frac{1}{3!}(\phi^{\wedge})^3+\cdots
$$
这里出现了无穷多指数幂,需要找到一种方式使得指数映射的计算简化
由于$\phi$是三维向量,也可以按照此方式定义它的模长θ与方向向量a($\left | a \right | = \sqrt{a_1^2+a_2^2+a_3^2}=1 $)。因此三维向量可以用模长和方向两个值表示,于是有$\phi=\theta a$。
对于a^,有以下两条性质:
-
性质一
$$
a^{\wedge}a^{\wedge}=
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}\\=
\begin{bmatrix}
-a_2^2-a_3^2 & a_1a_2 & a_1a_3 \\
a_1a_2 & -a_1^2-a_3^2 & a_2a_3 \\
a_1a_3 & a_2a_3 & -a_1^2-a_2^2
\end{bmatrix}\\=
\begin{bmatrix}
a_1^2-1 & a_1a_2 & a_1a_3 \\
a_1a_2 & a_2^2-1 & a_2a_3 \\
a_1a_3 & a_2a_3 & a_3^2-1
\end{bmatrix}\\=
\begin{bmatrix}
a_1a_1 & a_1a_2 & a_1a_3 \\
a_1a_2 & a_2a_2 & a_2a_3 \\
a_1a_3 & a_2a_3 & a_3a_3
\end{bmatrix}-
\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}\\=
\begin{bmatrix}
a_1\\
a_2\\
a_3
\end{bmatrix}
\begin{bmatrix}
a_1 & a_2 & a_3
\end{bmatrix}-I\\=
aa^T-I\
I=aa^T-a^{\wedge}a^{\wedge}
$$
上述推导过程利用了单位方向向量长度为1 -
性质二,参考性质一的结论:
$$
a^{\wedge}a^{\wedge}a^{\wedge}=(aa^T-I)a^{\wedge}=
aa^Ta^{\wedge}-a^{\wedge}\\=
\begin{bmatrix}
a_1a_1 & a_1a_2 & a_1a_3 \\
a_1a_2 & a_2a_2 & a_2a_3 \\
a_1a_3 & a_2a_3 & a_3a_3
\end{bmatrix}
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}-
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}\\=
\begin{bmatrix}
a_1a_2a_3-a_1a_2a_3 & a_1a_1a_3-a_1a_1a_3 & a_1a_1a_2-a_1a_1a_2\\
a_2a_2a_3-a_2a_2a_3 & a_1a_2a_3-a_1a_2a_3 & a_1a_2a_2-a_1a_2a_2\\
a_2a_3a_3-a_2a_2a_3 & a_1a_3a_3-a_1a_1a_3 & a_1a_2a_3-a_1a_2a_3
\end{bmatrix}\\-
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}\\=
\begin{bmatrix}
0 & -a_3 & a_2 \\
a_3 & 0 &-a_1 \\
-a_2 & a_1 & 0
\end{bmatrix}\\=
-a^{\wedge}
$$
通过观察上述式子,我们还可以总结得出以下式子:
$$
a^{\wedge}a^{\wedge}a^{\wedge}a^{\wedge}=-a^{\wedge}a^{\wedge}\\
a^{\wedge}a^{\wedge}a^{\wedge}a^{\wedge}a^{\wedge}=-a^{\wedge}a^{\wedge}a^{\wedge}=a^{\wedge}
$$
所以,我们可以得出:
$$
e^{\phi^{\wedge}}=e^{\theta a}=\sum^{\infty}_{n=0}\frac{1}{n!}(\theta a^{\wedge})^n\\=
I+\theta a^{\wedge}+\frac{1}{2!}(\theta a^{\wedge})^2+\frac{1}{3!}(\theta a^{\wedge})^3+\cdots\\=
I+\theta a^{\wedge}+\frac{\theta^2}{2!}(a^{\wedge})^2+\frac{\theta^3}{3!}(a^{\wedge})^3+\cdots\\=
I+\theta a^{\wedge}+\frac{\theta^2}{2!}a^{\wedge}a^{\wedge}+\frac{\theta^3}{3!}a^{\wedge}a^{\wedge}a^{\wedge}+\cdots
$$
将上述性质一$I=aa^T-a^{\wedge}a^{\wedge}$和性质二$a^{\wedge}a^{\wedge}a^{\wedge}=-a^{\wedge}$代入上式,进行反复嵌套可得:
$$
e^{\phi^{\wedge}}=aa^T-a^{\wedge}a^{\wedge}+\theta a^{\wedge}+\frac{\theta^2}{2!}a^{\wedge}a^{\wedge}-\frac{\theta^3}{3!}a^{\wedge}-\frac{\theta^4}{4!}a^{\wedge}a^{\wedge}\\+\frac{\theta^5}{5!}a^{\wedge}+\frac{\theta^6}{6!}a^{\wedge}a^{\wedge}-\frac{\theta^7}{7!}a^{\wedge}+\cdots
\\=
aa^T+(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots)a^{\wedge}
\\-(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+\cdots)a^{\wedge}a^{\wedge}
$$
而其中$(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots)$和$(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+\cdots)$分别是三角函数sin(a)和cos(a)的泰勒展开,因此可得:
$$
e^{\phi^{\wedge}}=
aa^T+(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots)a^{\wedge}
\\-(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+\cdots)a^{\wedge}a^{\wedge}\\=
I+a^{\wedge}a^{\wedge}+\sin\theta a^{\wedge}-\cos\theta a^{\wedge}\\=
(1-\cos\theta)a^{\wedge}a^{\wedge}+I+\sin\theta a^{\wedge}\\=
(1-\cos\theta)(aa^T-I)+I+\sin\theta a^{\wedge}\\=
(\cos\theta-1)I+(1-\cos\theta)aa^T+I+\sin\theta a^{\wedge}\\=
\cos\theta I+(1-\cos\theta)aa^T+\sin\theta a^{\wedge}
$$
聪明的你马上就能联想到第一篇我们讨论过的罗德里格斯公式。这说明,李代数so(3)就是旋转向量组成的向量空间,而这里的指数映射关系就是罗德里格斯公式。
通过它们,我们把so(3)中任意一个向量对应一个位于SO(3)中的旋转矩阵。反之,若定义与指数映射对应的对数映射,也能把SO(3)中的元素对应到so(3)中:
$$
\phi=\ln\left (R\right )^{\vee}=\left( \sum^{\infty}_{n=0}(R-I)^{(n+1)} \right)^{\vee}
$$
用泰勒展开求解挺麻烦的,另一种方式是如第一篇提到的利用旋转矩阵的迹tr()的性质求解旋转角与旋转轴。也就是对转角取两边的迹,然后化简计算。过程在第一篇文章中,这里只给出最后计算结果了:
$$
\theta=\arccos\frac{tr\left (R\right )-1}{2}
$$
2、SE(3)上指数映射
对于变换矩阵特殊欧氏群:
$$
SE(3)=\left \{ T=
\begin{bmatrix}
R & t\\
0^{T} & 1
\end{bmatrix}
\in \mathbb R^{4 \times 4} |
R\in SO(3),t\in \mathbb R^{3}
\right \}
$$
对应的李代数:
$$
\mathfrak{se}(3)=\left\{ \xi =
\begin{bmatrix}
\rho \\
\phi
\end{bmatrix}
\in \mathbb R^6
,\rho\in\mathbb R^3,\phi\in\mathfrak{so}(3),
\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge} & \rho \\
0^T & 0
\end{bmatrix}
\in\mathbb{R}^{4\times 4}
\right\}
$$
模仿上述李代数so(3)的元素的指数映射推导过程,李代数se(3)的指数映射证明如下:
已知
$$
\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}
$$
有:
$$
(\xi^{\wedge})^2=\xi^{\wedge}\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}=
\begin{bmatrix}
(\phi^{\wedge})^2&\phi^{\wedge}\rho\\
0^T&0
\end{bmatrix}\\
(\xi^{\wedge})^3=\xi^{\wedge}\xi^{\wedge}\xi^{\wedge}=
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}
\begin{bmatrix}
\phi^{\wedge}&\rho\\
0^T&0
\end{bmatrix}=
\begin{bmatrix}
(\phi^{\wedge})^3&(\phi^{\wedge})^2\rho\\
0^T&0
\end{bmatrix}
$$
总结规律得:
$$
(\xi^{\wedge})^n=
\begin{bmatrix}
(\phi^{\wedge})^n&(\phi^{\wedge})^{(n-1)}\rho\\
0^T&0
\end{bmatrix}
$$
接着我们讨论要求的指数映射式子:
$$
e^{\xi^{\wedge}}=\sum_{n=0}^{\infty}\frac{1}{n!}(\xi^{\wedge})^n\\
=I_{4\times 4}+\sum_{n=1}^{\infty}\frac{1}{n!}(\xi^{\wedge})^n\\=
\begin{bmatrix}
I_{3\times 3}&0\\
0^T&1
\end{bmatrix}+
\sum_{n=1}^{\infty}\frac{1}{n!}
\begin{bmatrix}
(\phi^{\wedge})^n&(\phi^{\wedge})^{(n-1)}\rho\\
0^T&0
\end{bmatrix}\\=
\begin{bmatrix}
\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n&\sum_{n=1}^{\infty}\frac{1}{n!}(\phi^{\wedge})^{(n-1)}\rho\\
0^T&1
\end{bmatrix}\\=
\begin{bmatrix}
\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n&\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^{n}\rho\\
0^T&1
\end{bmatrix}
$$
因此:
$$
e^{\xi^{\wedge}}=
\begin{bmatrix}
\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n&\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^{n}\rho\\
0^T&1
\end{bmatrix}\triangleq
\begin{bmatrix}
R & J\rho \\
0^T & 1
\end{bmatrix}=T
$$
其中,指数映射左上角R为旋转矩阵,是李群SO(3)中的元素
$$
R=\sum_{n=0}^{\infty}\frac{1}{n!}(\phi^{\wedge})^n
$$
与特殊欧氏变换群对应李代数se(3)的旋转部分$\phi$相对应。
右上角J的部分的具体内容与上述SO(3)上指数映射证明过程类似,也进行泰勒展开,并同样地,三维向量$\phi$的模长为$\theta$,单位方向向量为a,则$\phi=\theta a$。
$$
J = \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^n\\=
I+\frac{\theta}{2!}a^{\wedge}+\frac{\theta^2}{3!}(a^{\wedge})^2
+\frac{\theta^3}{4!}(a^{\wedge})^3+\frac{\theta^4}{5!}(a^{\wedge})^4
+\cdots\\=
I+\frac{\theta}{2!}a^{\wedge}+\frac{\theta^2}{3!}(a^{\wedge})^2
-\frac{\theta^3}{4!}a^{\wedge}-\frac{\theta^4}{5!}(a^{\wedge})^2
+\cdots\\=
I+(\frac{\theta}{2!}-\frac{\theta^3}{4!}+\cdots)a^{\wedge}+
(\frac{\theta^2}{3!}-\frac{\theta^4}{5!}+\cdots)(a^{\wedge})^2
\\=
I+\frac{1}{\theta}(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\cdots)a^{\wedge}+
\frac{1}{\theta}(\frac{\theta^3}{3!}-\frac{\theta^5}{5!}+\cdots)(a^{\wedge})^2
$$
而其中三角函数sin(a)和cos(a)的泰勒展开:
$$
\sin\theta=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots\\
\cos\theta=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+\cdots
$$
所以:
$$
\theta-\sin\theta=\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots\\
1-\cos\theta=\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+\cdots
$$
用来代入上式得:
$$
J = \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^n\\=
I+\frac{1}{\theta}(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\cdots)a^{\wedge}+
\frac{1}{\theta}(\frac{\theta^3}{3!}-\frac{\theta^5}{5!}+\cdots)(a^{\wedge})^2\\=
I+\frac{1-\cos\theta}{\theta}a^{\wedge}+\frac{\theta-\sin\theta}{\theta}(a^{\wedge})^2
$$
又因为前面提到的性质一:
$$
I=aa^T-a^{\wedge}a^{\wedge}\\
aa^T=a^{\wedge}a^{\wedge}-I
$$
代入得:
$$
J = \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^n\\=
I+\frac{1}{\theta}(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\cdots)a^{\wedge}+
\frac{1}{\theta}(\frac{\theta^3}{3!}-\frac{\theta^5}{5!}+\cdots)(a^{\wedge})^2\\=
I+\frac{1-\cos\theta}{\theta}a^{\wedge}+\frac{\theta-\sin\theta}{\theta}(a^{\wedge}a^{\wedge}-I)
\\=
\frac{\sin\theta}{\theta}I+\frac{1-\cos\theta}{\theta}a^{\wedge}+\frac{\theta-\sin\theta}{\theta}aa^T
$$
因此李代数右上角$\xi^{\wedge}$的平移部分经过矩阵的指数映射操作后,进行了以J为系数的线性变换。
相反地,根据变换矩阵T想求出对应李代数so(3)上的向量,可以从T左上角的旋转矩阵来计算旋转向量,T右上角满足:
$$
t=J\rho
$$
由于 J 可以由 Φ 得到,所以这里的 ρ 也可以由该线性方程得到。
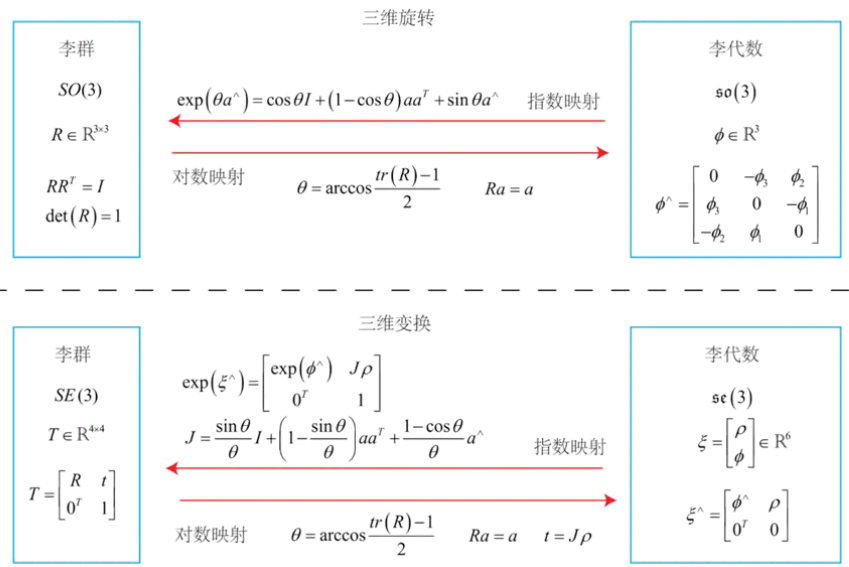
综上,其对应关系汇总在下方了:
四、李代数求导与扰动模型
1、BCH公式与近似形式:
使用李代数的一大动机是进行优化,而在优化的过程中,导数是非常重要的。
由于SO(3) SE(3)上李群李代数之间存在一对一的转换关系
那当李群中完成两个矩阵相乘时候,对应李代数会发生什么? 以及李代数中完成两个向量元素的相加的结果,对应到李群中是不是两个矩阵的乘积?
也就是$e^{\phi_1^{\wedge}}e^{\phi_2^{\wedge}}=e^{(\phi_1+\phi_2)^{\wedge}}$是否成立。
当$\theta_1,\theta_2$是标量数字的时候,这个等式成立。但当他们是矩阵的时候,就变成了矩阵的指数函数,这个等式是不成立的:
$$
\ln(e^{\phi_!^{\wedge}}e^{\phi_2^{\wedge}})^{\vee}\ne\phi_1+\phi_2
$$
两个李代数指数映射成绩的完整形式,由 (Baker-Campbell-Hausdorff, BCH)公式给出,是群论和量子力学中常用的公式之一,其展开式的前几项为:
$$
\ln(e^{A}e^{B})=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[A,[A,B]]+\cdots
$$
上式右侧的[]符号是两个矩阵之间的李括号运算,可以看出两个矩阵指数的乘积,会产生很多李括号组成的余项。
特别的,考虑SO(3)上的李代数$\ln(e^{\phi_1^{\wedge}})$,当$\phi_1$或$\phi_2$其中一个是值非常小的向量的时候,那么公式右侧二次以上的余项几乎可以忽略不计。因此BCH公式可以近似表达为:
$$
\ln(e^{\phi_!^{\wedge}}e^{\phi_2^{\wedge}})^{\vee}\approx
\begin{cases}
J_l(\phi_2)^{-1}\phi_1+\phi_2,当\phi_1为小量 \\
J_r(\phi_1)^{-1}\phi_2+\phi_1,当\phi_2为小量
\end{cases}
$$
-
第一种情况是,当旋转矩阵R2(其对应的李代数为Φ2),左乘一个很小的旋转矩阵R1(其对应的李代数为Φ1),那么可以近似看做,在原有的李代数Φ2基础上加一项$J_l(\phi_2)^{-1}\phi_1$
-
第二种情况是,右乘一个比较小的微小位移的情况
-
第一种是左乘BCH近似,第二种是右乘BCH近似,对应左乘模型和右乘模型
这里的左乘BCH近似中的雅克比$j_l$就是第三节中,李代数向量$\xi$的指数映射$e^{\xi^{\wedge}}=\begin{bmatrix}R & J\rho\\0^{T} & 1\end{bmatrix}$。
令$\phi$的模长为$\theta$,单位方向向量为a,则$\phi=\theta a$,右上角的那个雅克比矩阵经过泰勒展开后可得:
$$
J_l=J=\sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^{\wedge})^n
\\=
\frac{\sin\theta}{\theta}I+\frac{1-\cos\theta}{\theta}a^{\wedge}+\frac{\theta-\sin\theta}{\theta}aa^T
$$
再取其逆:
$$
J_l^{-1}=\frac{\theta}{2}\cot\frac{\theta}{2}I-\frac{\theta}{2}a^{\wedge}+(1-\frac{\theta}{2}\cot\frac{\theta}{2})aa^T
$$
而右乘雅克比仅需要对自变量取负号即可:
$$
J_r(\phi)=J_l(-\phi)
$$
这样下来,我们就可以讨论李群乘法与李代数加法的关系了。
为了便于理解,这里咱重新讨论一下BCH近似的意义:
假定对某个旋转R,对应的李代数为Φ,我们给他左乘一个微小旋转,记作△R,对应的李代数为△Φ。
那么,在李群上,得到的结果为两个矩阵相乘△R·R,那么对应的李代数△Φ为小量。根据左乘BCH近似,为$J_l(\phi)^{-1}\Delta \phi+\phi$(在微量旋转前左乘一个雅克比矩阵的逆)。合并起来的话,两个李代数指数映射乘积的完整形式可以写成:(复杂式子写在e指数上面显得好小啊看不清。。。)
$$
e^{\Delta\phi^{\wedge}}e^{\phi^{\wedge}}=\exp{\left((\phi+J_l^{-1}(\phi)\Delta\phi)^{\wedge}\right)}
$$
如果微量旋转在上式左边的右侧,就采用右乘近似,
$$
e^{\phi^{\wedge}}e^{\Delta\phi^{\wedge}}=\exp{\left((\phi+J_r^{-1}(\phi)\Delta\phi)^{\wedge}\right)}
$$
反之,若我们在李代数上进行加法,让一个Φ加上△Φ,那么可以近似为李群上带左右雅克比的乘法:
$$
e^{(\phi+\Delta\phi)^{\wedge}}=e^{(J_l\Delta\phi)^{\wedge}}e^{\phi^{\wedge}}=e^{\phi^{\wedge}}e^{(J_r\Delta\phi)^{\wedge}}
$$
上式为李代数做微积分打基础用的。
同样的,在特殊欧氏群SE(3)也有类似的BCH近似:
$$
e^{\Delta\xi^\wedge}e^{\xi^\wedge}\approx\exp\left((\mathcal{J} _l^{-1}\Delta\xi+\xi)^\wedge\right)
$$
若微量选逆转正在上式左边的右侧,则采用右乘近似:
$$
e^{\xi^\wedge}e^{\Delta\xi^\wedge}\approx\exp\left((\mathcal{J} _r^{-1}\Delta\xi+\xi)^\wedge\right)
$$
因为这里${\mathcal{J_l}}$的形式比较复杂,它是一个6×6的一个矩阵,由于很复杂,后续也不咋用到,想了解可以看看这本书中式子(7.82)与(7.83)
🔖 T. Barfoot, “State estimation for robotics: A matrix lie group approach,” 2016.
2、SO(3)上的李代数求导
在SLAM中,需要估计一个相机的位置和姿态,位姿由李群特殊正交群SO(3) 上的旋转矩阵或者李群特殊欧式群SE(3) 上的变换矩阵进行描述的。
设机器人某个时刻的位姿为T,它观察到一个世界坐标,位于p点,还产生了一个数据z,那么,由坐标变换的关系可得:
$$
z=Tp+w
$$
w为随机的噪声,由于噪声的存在,观测数据的结果z一般来说不可能精确的满足z=Tp的关系。所以,我们会计算理想的观色与实际数据的误差:
$$
error=z-Tp
$$
假设一共有N个这样的路标点(Landmarks)和观测数据(Observation),就会有N个误差公式,计算出N个结果。
那么对于机器人进行位姿估计,相当于要找一个最优的T,使得整体误差最小化:
$$
\min_{T}J(T)=\sum_{i=1}^{N}\left|z_i-Tp_i\right|^2_2
$$
要求解这个问题,需要计算目标函数J关于变换矩阵T的导数了,具体算法后面再说吧,这里的重点在于,我们经常会构建与位姿有关的函数,然后谈论该函数关于位姿的导数,用以调整当前的估计值。
but,SO(3)和SE(3)对于加法运算是不封闭的,也就是说,两个旋转矩阵相加就不再是旋转矩阵了,因此如果需要在李群上进行后续的优化,需要加上不少约束条件,比如说旋转矩阵的正交性啦,行列式为1等等,给优化过程添不少堵。而李代数是由向量组成的,能够进行良好的加法运算。
所以说,解决求导问题的思路主要有以下两种:
- 用李代数表示姿态,然后根据李代数加法对李代数求导,对应李代数的求导模型
- 对李群左乘或右乘微小扰动,然后对这个扰动求导,称为左扰动和右扰动模型,对应扰动模型
3、李代数求导
首先考虑SO(3)的情况。假设我们对一个空间点p进行旋转,得到Rp,现在,要计算旋转之后的点坐标相对于旋转的导数,我们简单记为:
$$
\frac{\partial (Rp)}{\partial R}
$$
要注意的是,这里不能按照矩阵微分来定义导数,只是一个便于理解的记号
由于SO(3)没有加法,所以这个导数没办法按照导数的定义进行计算。设R对应的李代数为Φ,我们去计算:
$$
\frac{\partial (Rp)}{\partial R}=
\frac{\partial e^{\phi^{\wedge}}p}{\partial R}
=\lim_{\delta\phi\to0}\frac{e^{(\phi+\delta\phi)^{\wedge}}p-e^{\phi^{\wedge}}p}{\delta\phi}
$$
严格按照矩阵微分来说,智能邱行向量关于列向量的导数,结果为一个矩阵。这里写成列向量对列向量的导数,可以认为先对分子进行转置,再对最后结果进行转置,这样使得公式简洁易读,不然就得为每行的分子加一个转置符号
由于指数函数exp(x)的泰勒展开为:
$$
e^X=1+X+\frac{X^2}{2!}+\frac{X^3}{3!}+\cdots
$$
由于这里的指数部分为矩阵,且$\Delta\phi\to0$,因此泰勒级数展开式二次以上的高阶项可以忽略不计:
$$
e^{(J_l\Delta\phi)\wedge}=\sum_{n=0}^{\infty}\frac{1}{n!}((J_l\Delta\phi)^\wedge)
\\=
I+(J_l\Delta\phi)^\wedge
+
\frac{((J_l\Delta\phi)^\wedge)^2}{2!}
+
\frac{((J_l\Delta\phi)^\wedge)^3}{3!}
+\cdots
\approx I+(J_l\Delta\phi)^\wedge
$$
代入上式可得:
$$
\frac{\partial (Rp)}{\partial R}=
\frac{\partial e^{\phi^{\wedge}}p}{\partial R}
=\lim_{\delta\to0}\frac{e^{(\phi+\delta\phi)^{\wedge}}p-e^{\phi^{\wedge}}p}{\delta\phi}
\\\approx
\lim_{\delta\phi\to 0}
\frac{(I+(J_l\Delta\phi)^\wedge)e^{\phi^{\wedge}}p-e^{\phi^{\wedge}}p}{\delta\phi}
\\=
\lim_{\delta\phi\to 0}
\frac{(J_l\Delta\phi)^\wedge e^{\phi^{\wedge}}p}{\delta\phi}
$$
到这里,在利用叉乘和反对称矩阵的性质.
因为$(J_l\Delta\phi)^\wedge$是反对称矩阵,$e^{\phi^{\wedge}}p$是一个向量,两个向量 a,b相叉乘等价于向量的反对称矩阵乘向量$a\times b=a^{\wedge}b$。而由于叉乘运算是不满足交换律的,两个向量互换位置的时候要加个负号:
$$
a\times b=-b\times a
$$
所以,上式可以调整为:
$$
\frac{\partial e^{\phi^{\wedge}}p}{\partial R}=
\lim_{\delta\phi\to 0}
\frac{(J_l\Delta\phi)^\wedge e^{\phi^{\wedge}}p}{\delta\phi}
\\=
\lim_{\delta\phi\to 0}
\frac{(J_l\Delta\phi)\times (e^{\phi^{\wedge}}p)}{\delta\phi}
\\=
\lim_{\delta\phi\to 0}
\frac{-(e^{\phi^{\wedge}}p)\times(J_l\Delta\phi)}{\delta\phi}
\\=
\lim_{\delta\phi\to 0}
\frac{-(e^{\phi^{\wedge}}p) ^\wedge (J_l\Delta\phi)}{\delta\phi}
$$
由导数定义可得:
$$
\frac{\partial e^{\phi^{\wedge}}p}{\partial R}=
\lim_{\delta\phi\to 0}
\frac{-(e^{\phi^{\wedge}}p) ^\wedge (J_l\Delta\phi)}{\delta\phi}=
-(Rp)^\wedge J_l
$$
证到这里,就得到了旋转后点 Rp 相对于李代数的导数,结果中存在一个左雅克比矩阵Jl,计算该矩阵比较麻烦一点,需要介绍扰动模型来给出更简单的李代数求导方法。
4、左乘扰动模型
另一种李代数的求导方式是对旋转矩阵进行一次扰动△R,然后看结果中相对于该扰动的变化率。
这个扰动可以乘左边或右边,结果会有点差别。
我们以左扰动为例:
设左扰动△R对应的李代数 δφ,然后对该李代数 δφ 进行求导。根据导数定义:
$$
\frac{\partial (Rp)}{\partial R}=
\frac{\partial(\Delta RR_p)}{\partial (\Delta R)}=
\frac{\partial(e^{(\delta\varphi)^\wedge}e^{\phi^{\wedge}}p)}{\partial (\delta\varphi)}
\\=
\lim_{\delta\varphi\to0}\frac{e^{(\delta\varphi)^\wedge} e^{\phi^\wedge}p-e^0e^{\phi^{\wedge}}p}{\delta\varphi-0}
\\\approx
\lim_{\delta\varphi\to0}\frac{(I+(\delta\varphi)^\wedge)e^{\phi^{\wedge}}p-e^{\phi^{\wedge}}p}{\delta\varphi}
\\=
\lim_{\delta\varphi\to0}\frac{(\delta\varphi)^\wedge(e^{\phi^\wedge}p)}{\delta\varphi}
\\=
\lim_{\delta\varphi\to0}\frac{-(e^{\phi^\wedge}p)^\wedge (\delta\varphi)}{\delta\varphi}
\\=
-(e^{\phi^\wedge}p)^\wedge=-(Rp)^\wedge
$$
相比较对旋转矩阵对应的李代数直接进行求导,这里对扰动模型的求导少了一个雅各比矩阵的计算,大大的简便了求导的过程,更加方便使用。
5、SE(3)上的李代数求导
这里不再是直接对李代数求导,因为扰动模型求导更加简便实用,直接给出特殊欧式群上左乘或者右乘微小的扰动,再对该扰动进行求导(左右扰动模型)
假设三维空间点p经过一次特殊欧式群SE(3)中的变换矩阵$T\in\mathbb{R}^{4\times 4}$(旋转+平移),其对应李代数so(3)上的六维向量$\xi\in\mathbb{R}^6$,该空间点经过变换后的点坐标为Tp(p为齐次坐标$p=\begin{bmatrix}\bar{p}\\1\end{bmatrix}$),相对于变换T的导数,由于李群上无法按照导数的定义进行计算,转为直接给变换T增加一个微小扰动$\Delta T=e^{(\delta\xi)^\wedge}$,则扰动项的李代数为$\delta\xi=\begin{bmatrix}\delta\rho \\delta\phi\end{bmatrix}$。
$$
\frac{\partial (Tp)}{\partial T}=
\frac{\partial(\Delta TT_p)}{\partial (\Delta T)}=
\frac{\partial(e^{(\delta\xi)^\wedge}e^{\xi^{\wedge}}p)}{\partial (\delta\xi)}
\\=
\lim_{\delta\xi\to0}\frac{e^{(\delta\xi)^\wedge} e^{\xi^\wedge}p-e^0e^{\xi^{\wedge}}p}{\delta\xi-0}
$$
继续利用指数函数的泰勒展开代入:
$$
\lim_{\delta\xi\to0}\frac{e^{(\delta\xi)^\wedge} e^{\xi^\wedge}p-e^0e^{\xi^{\wedge}}p}{\delta\xi-0}
\\\approx
\lim_{\delta\xi\to0}\frac{(I+(\delta\xi)^\wedge)e^{\xi^{\wedge}}p-e^{\xi^{\wedge}}p}{\delta\xi}
\\=
\lim_{\delta\xi\to0}\frac{(\delta\xi)^\wedge(e^{\xi^\wedge}p)}{\delta\xi}
$$
由于这里变换矩阵中的符号^不是反对称的意思,而是“六维向量转换为四维矩阵”的意思,我们前面有提到的,所以这里不能继续利用叉积的性质进行推导了.
$$
由于\delta\xi=
\begin{bmatrix}\delta\rho \\\delta\phi\end{bmatrix},
(\delta\xi)^\wedge=
\begin{bmatrix}
\delta\phi^\wedge & \delta\rho\\
0^T & 0
\end{bmatrix}
\\
e^{\xi^\wedge}=Tp=
\begin{bmatrix}
R & J\rho \\
0^T & 1
\end{bmatrix}
\begin{bmatrix}\bar{p}\\1\end{bmatrix}=
\begin{bmatrix}
R\bar{p}+J\rho\\
1
\end{bmatrix}
\\=
\lim_{\delta\xi\to0}\frac{(\delta\xi)^\wedge(e^{\xi^\wedge}p)}{\delta\xi}
\\=
\lim_{\delta\xi\to0}\frac{
\begin{bmatrix}
\delta\xi & \delta\rho \\
0^T & 0
\end{bmatrix}
\begin{bmatrix}
R\bar{p}+J\rho\\
1
\end{bmatrix}
}{\delta\xi}
\\=
\lim_{\delta\rho\to0,\delta\phi\to0}
\frac{
\begin{bmatrix}
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho\\
1
\end{bmatrix}
}{
\begin{bmatrix}
\delta\rho\\
\delta\phi
\end{bmatrix}
}
$$
上式为矩阵除法,分子是 4×1 的行向量,分母是 1×6 的列向量,结果应该是 4×6 的矩阵,这里涉及到矩阵求导顺序的问题,比如假设a,b,x,y都是列向量,那么矩阵求导的写法如下:
$$
\frac{\mathrm{d}
\begin{bmatrix}
a\\b
\end{bmatrix}
}{\mathrm{d}
\begin{bmatrix}
x\\y
\end{bmatrix}
}=
\left(
\frac{\mathrm{d}
\begin{bmatrix}
a,b
\end{bmatrix}^T
}{\mathrm{d}
\begin{bmatrix}
x\\y
\end{bmatrix}
}
\right)=
\begin{bmatrix}
\frac{\mathrm{d}a}{\mathrm{d}x} &
\frac{\mathrm{d}b}{\mathrm{d}x}\\
\frac{\mathrm{d}a}{\mathrm{d}y} &
\frac{\mathrm{d}b}{\mathrm{d}y}\\
\end{bmatrix}^T=
\begin{bmatrix}
\frac{\mathrm{d}a}{\mathrm{d}x} &
\frac{\mathrm{d}a}{\mathrm{d}y}\\
\frac{\mathrm{d}b}{\mathrm{d}x} &
\frac{\mathrm{d}b}{\mathrm{d}y}\\
\end{bmatrix}
$$
因此上式中的矩阵除法也可以这样操作:
$$
令da=\delta\phi(R\bar{p}+Jp)+\delta\rho,db=0^T,dx=\delta\rho,dy=\delta\phi
\\
\lim_{\delta\rho\to0,\delta\phi\to0}
\frac{
\begin{bmatrix}
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho\\
1
\end{bmatrix}
}{
\begin{bmatrix}
\delta\rho\\
\delta\phi
\end{bmatrix}
}
\\=
\lim_{\delta\rho\to0,\delta\phi\to0}
\begin{bmatrix}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\rho}
&
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\phi}
\\
0^T & 0^T
\end{bmatrix}
\\=
\begin{bmatrix}
\lim_{\delta\rho\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\rho}
&
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\phi}
\\
0^T & 0^T
\end{bmatrix}
$$
由于该矩阵左上角的$\delta\phi^{\wedge}(R\bar{p}+J\rho)$部分与$\delta\rho$无关,常量关于$\delta\rho$的导数为0,所以有:
$$
\lim_{\delta\rho\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\rho} =I
$$
同理,右上角的$\delta\rho$与$\delta\phi$无关,其关于$\delta\phi$的导数为0:
$$
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\phi}=
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)
}{\delta\phi}
$$
到了这里,符号^就是反对称矩阵的意思了,直接用叉积和反对称符号的性质可得:
$$
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\phi}
\\=
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)
}{\delta\phi}
\\=
\lim_{\delta\phi\to0}
\frac{
-(R\bar{p}+J\rho)^{\wedge}\delta\phi
}{\delta\phi}
\\=
-(R\bar p+J\rho)^{\wedge}
$$
最终这两项代回去,可得:
$$
\begin{bmatrix}
\lim_{\delta\rho\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\rho}
&
\lim_{\delta\phi\to0}
\frac{
\delta\phi^{\wedge}(R\bar{p}+J\rho)+\delta\rho
}{\delta\phi}
\\
0^T & 0^T
\end{bmatrix}
\\=
\begin{bmatrix}
I & -(R\bar p+J\rho)^{\wedge}\\
0^T & 0^T
\end{bmatrix}
$$
可以使用符号$\odot $来表示上述结论:
$$
(Tp)^\odot =
\begin{bmatrix}
I & -(R\bar p+J\rho)^{\wedge}\\
0^T & 0^T
\end{bmatrix}_{4\times6}
$$
这个符号$\odot $的几何意义是:三维空间点的其次坐标$p=\begin{bmatrix}\bar{p}\\1\end{bmatrix}$进过一次变换T之后,变成了一个4×6的矩阵。
恭喜你坚持看到这里🎉,我们完成了李群李代数上相关的微分计算🎉
五、相似变换群与李代数
这里是为了 “简单” 补充一下有关单目视觉中使用的相似变换群Sim(3),以及对应的李代数$\mathfrak{sim}(3)$。只对双目SLAM或RGB-D SLAM感兴趣可以先跳过~
这里需要先说明一个点,就是单个摄像头固定住的话,是没办法估计事物的距离的。好比单只眼睛是无法直接获取深度信息

单目相机不论远近,看到的图像信息是一样的,这对建图很不利,我们先称之为尺度不确定性,具体会在后续文章介绍。
并且,仅靠相机里程计估计轨迹,将不可避免出现累计漂移,简单说就是地图建歪了。这个还需要后端优化和回环检测来矫正。这个也是后续再说。
所以说,如果在单目SLAM中使用SE(3)表示位姿,那么由于尺度不确定性与尺度漂移,整个SLAM过程中的尺度会发生一些变换,这在SE(3)中没办法体现出来。
单目情况下,我们一般会显示地将尺度因子表达出来。用数学语言来说的话就是,对于位于空间点p,在相机坐标系下要经过一个相似变换
$$
P’=
\begin{bmatrix}
sR & t\\
0^T & 1
\end{bmatrix}
p=
sRp+t
$$
在相似变换中,我们把这个尺度s表达出来了。它同时作用在p的三个坐标上,对p进行了一次缩放。与SO(3)和SE(3)相似,相似变换也对矩阵乘法构成群,叫做相似变换群Sim(3).
$$
Sim(3)=
\left\{
S=
\begin{bmatrix}
sR & t\\
0^T & 1
\end{bmatrix}
\in\mathbb{R}^{4\times 4}
\right\}
$$
同样的,Sim(3)也有对应的李代数、指数映射、对数映射等等。李代数sim(3)元素是一个7维的向量$\zeta$。它前6维与se(3)相同,就是最后多一项$\sigma$。
$$
\mathfrak{sim}(3)
\left\{
\zeta|\zeta=
\begin{bmatrix}
\rho\\\phi\\\sigma
\end{bmatrix}
\in\mathbb R^7,
\zeta^\wedge=
\begin{bmatrix}
\sigma I+\phi^{\wedge} & \rho \\
0^T & 0
\end{bmatrix}\in\mathbb R^{4\times4}
\right\}
$$
它比se(3)多了一项σ,关联Sim(3)与sim(3)的仍是指数映射与对数映射。
指数映射:
$$
e^{(\zeta^{\wedge})}=
\begin{bmatrix}
e^\rho e^{\phi^\wedge} & J_s\rho\\
0^T & 1
\end{bmatrix}
$$
其中J的形式为:
$$
J=\frac{e^\sigma-1}{\sigma}I+
\frac{\sigma e^\sigma\sin\theta+(1-e^\rho\cos\theta)\theta}{\sigma^2+\theta^2}a^\wedge
\\+(\frac{e^\sigma-1}{\sigma}-
\frac{\sigma (e^\sigma\cos\theta-1)+(e^\sigma\sin\theta)\theta}{\sigma^2+\theta^2}
)a^\wedge a^\wedge
$$
对于李代数$\zeta$,它与李群的对应关系为:
$$
s=e^\sigma,R=e^{\phi^\wedge},t=J_s\rho
$$
旋转部分上是和SO(3)一致的。平移部分,在se(3)中需要乘一个雅克比$\mathcal J$,而相似变换的雅克比更复杂。
对于尺度因子,可以看到李群中的s即为李代数中的σ的指数函数。
Sim(3)的BCH近似与SE(3)是类似的。存在微分模型和扰动模型两种方式,而扰动模型相较来说比较简单,以下是结果:
设给相似变换Sp左侧一个小扰动$\exp(\zeta^\wedge)$,并求Sp对于扰动的导数。因为Sp是4维的齐次坐标,$\zeta$则是7维向量,所以导数应该是4×7的雅克比。方便期间,记录Sp的前3维组成向量q,那么:
$$
\frac{\partial Sp}{\partial\zeta}=
\begin{bmatrix}
I & -q^\wedge & q\\
0^T & 0^T & 0
\end{bmatrix}
$$
本篇介绍的内容有点太多了,关于李群李代数的代码实现Sophus我们放在下一章做一个简单地补充



