警告:本篇含有大量数学公式,请尽量在网络良好的状态下访问
网络较差的情况下,数学公式渲染容易出问题
三维空间刚体运动基础
在机器人学中,有一个很重要的知识点叫做坐标系变换。
本篇将简单涉及一下坐标系的相关知识
我们日常生活中的空间是三维的,我们使用的坐标系如下图:
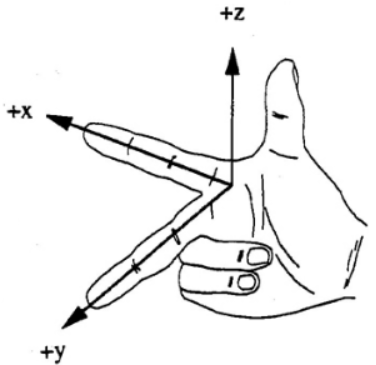
我们对坐标系的几点说明:
- 像题图那样的彩色坐标系,若无特别说明,都是rgb(红绿蓝)依次对应*xyz*
- 当我们说绕某一个轴旋转多少角度时,正方向的确定用右手定则,如下图:
- 我们用的都是右手坐标系,即绕z轴旋转时,y轴在x轴的+90度方向,其他轴类似,四指弯曲的方向即为正方向
- 提到某一个坐标系,比如坐标系A时,我们说frame{A},用大括号表示
- 提到任意需要指明参照系的量时,我们将坐标系写在左上角,如坐标系{A}中点P的位置向量写作$^{A}P$
- 我们将物体/点的名称写在右下角,如坐标系{A}中点O的位置向量写作$^{A}P_{O}$
- 提到一个量是相对于某个坐标系时,比如{A},我们说with respect to {A},或简写为w.r.t {A}。
- 本文及以后的文章中所有向量都是列向量,所有向量的转置都是行向量
- 以上是一套比较常用的标记系统(convention),始终遵循同一套convention有助于在混乱的坐标变换中找到清晰的思路;如果你已经有常用的记法,那么保持你自己的记法也是可以的
1、向量与坐标系
回到原题,我们用线性代数的知识来说,三维空间中某个点的坐标可以用$\mathbb R^{3}$来描述。我们找到该空间的一组基[1], 那么,任意向量a就有这么个坐标如下: $$ a = \begin{bmatrix} e1 & e2 & e3 \end{bmatrix} \begin{bmatrix} a1\\\\ a2\\\\ a3 \end{bmatrix} = a1e1 + a2e2 + a3e3 $$ 这里$(a1,a2,a3)^{T}$成为a在此基下的坐标。对于$a,b\in \mathbb R^{3}$,通常意义下的**内积**是: $$ a \cdot b = a^{T}b = \sum_{i=1}^{3}a_{i}b_{i}=|a||b|\cos \left \langle a,b \right \rangle $$ 其中$\left \langle a,b \right \rangle $为向量a,b的夹角。内积也可以描述向量间的投影关系,外积则是这样的 $$ a\times b = \begin{Vmatrix} e_{1} & e_{2} & e_{3}\\\\ a_{1} & a_{2} & a_{3}\\\\ b_{1} & b_{2} & b_{3} \end{Vmatrix} = \begin{bmatrix} a_{2}b_{3} - a_{3}b_{2}\\\\ a_{3}b_{1} - a_{1}b_{3}\\\\ a_{1}b_{2} - a_{2}b_{1} \end{bmatrix} = \begin{bmatrix} 0 & -a_{3} & a_{2}\\\\ a_{3} & 0 & -a_{1}\\\\ -a_{2} & a_{1} & 0 \end{bmatrix}b \overset{\mathrm{def}}{=} a^{\wedge} b $$
外积的结果是一个向量,方向垂直于这两个向量,大小是$|a||b|\sin \left \langle a,b \right \rangle $,是两个向量张成的四边形的有向面积。
外积运算我们用^符号来表示,把a写成一个矩阵,这就是反对称矩阵。反对称矩阵满足$A^{T} = -A$这样就把外积$a\times b$写成了矩阵与向量的乘法a^b,变成了线性运算。此符号是一个一一映射,也就是说,任意向量都有唯一一个反对称矩阵,反之亦然。
$$
a^{\wedge} =
\begin{bmatrix}
0 & -a_{3} & a_{2}\\
a_{3} & 0 & -a_{1}\\
-a_{2} & a_{1} & 0
\end{bmatrix}
$$
2、坐标系间欧式变换
在机器人学中,会给每一个连杆和关节定义他们的坐标系。如果考虑移动的机器人,常见的方法是设定一个世界坐标系,我们可以认为,他是不会移动的,如下图中的$x_{w},y_{w},z_{w}$定义的坐标系。同时,机器人是一个移动的坐标系,如$x_{c},y_{c},z_{c}$定义的坐标系。
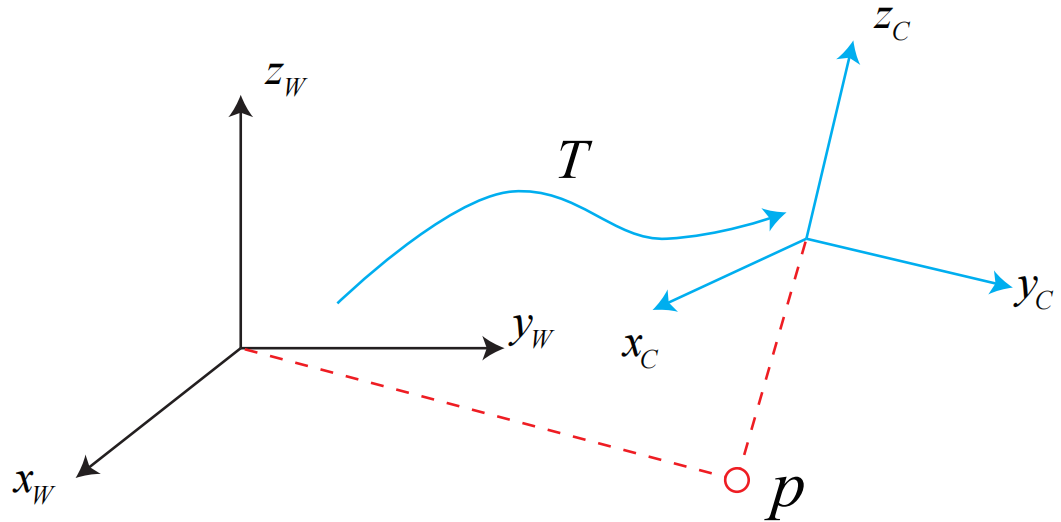
两个坐标系之间的运动由一个旋转加上一个平移组成,这种运动称之为刚体运动。相机在视界坐标系的运动就是一种刚体运动。刚体运动过程中,同一个向量在各个坐标系下的长度和夹角都不会改变。毕竟相机不会像棉花糖一样,会被压扁拉长,此时,我们说相机坐标系到世界坐标系之间,相差了一个欧式变换。
因为欧式变换由旋转和平移组成,我们先看一下旋转:
设某个单位正交基$(e_{1},e_{2},e_{3})$经过一次旋转变成$(e^{\backprime}_{1},e^{\backprime}_{2},e^{\backprime}_{3})$,那对同一个向量a(因为只讨论旋转,他也没运动),他在两个坐标系下的坐标是$[a_{1},a_{2},a_{3}]^{T}$和$[a^{\backprime}_{1},a^{\backprime}_{2},a^{\backprime}_{3}]^{T}$。因为向量本身没变,就有下列式子:

为了描述两个坐标之间的关系,对上面等式的左右两边同时左乘$\begin{bmatrix}
e_{1}^{T} \\
e_{2}^{T} \\
e_{3}^{T}
\end{bmatrix}$,那左边的系数就变成单位矩阵:
$$
\begin{bmatrix}
a_{1} \\
a_{2} \\
a_{3}
\end{bmatrix}=\begin{bmatrix}
e_{1}^{T}e_{1}^{\backprime} & e_{1}^{T}e_{2}^{\backprime} & e_{1}^{T}e_{3}^{\backprime}\\
e_{2}^{T}e_{1}^{\backprime} & e_{2}^{T}e_{2}^{\backprime} & e_{2}^{T}e_{3}^{\backprime}\\
e_{3}^{T}e_{1}^{\backprime} & e_{3}^{T}e_{2}^{\backprime} & e_{3}^{T}e_{3}^{\backprime}
\end{bmatrix}
\begin{bmatrix}
a_{1}^{\backprime} \\
a_{2}^{\backprime} \\
a_{3}^{\backprime}
\end{bmatrix}
\overset{\mathrm{def}}{=}Ra^{\backprime}
$$
中间3x3的矩阵拿出来,给他起名叫做R,这个矩阵有两组基之间的内积组成,说明了前后同一个向量的坐标变换关系。只要这个旋转操作一样,这个矩阵就是一样的,矩阵R描述了旋转本身,使用给他起个名字,叫旋转矩阵。
补充: 这个旋转矩阵,各分量是两个坐标系基的内积,因为基长度为1,所以实际上是各个积向量夹角的余弦值。所以这个矩阵也叫方向余弦矩阵。本篇还是将其称作旋转矩阵。
事实上,旋转矩阵是一个行列式为1的正交矩阵,那行列式为1的正交矩阵就是一个旋转矩阵。所以把n维旋转矩阵的集合定义如下:
$$
SO(n)=\left \{ R \in \mathbb R ^{n \times n} | RR^{T}=I,det(R)=1\right \}
$$
SO(n)是特殊正交群:
群是一种集合加上一种运算的代数结构,如果集合为A,运算为+,那么可以记为群G=(A , +)。群要求这个运算要满足以下几个条件:
封闭性:$\forall a,b \in A,a1 \cdot a2 \in A $
结合律:$\forall a,b,c \in A,(a1 \cdot a2)\cdot a3=a1 \cdot (a2 \cdot a3)$
幺元:$\exists a0 \in A,s.t. \forall a\in A,a_{0}\cdot a=a\cdot a_{0}=a$
逆:$\forall a \in A,\exists a^{-1} \in A, s.t.: a\cdot a^{-1}=a_{0}$
可以巧记为:封结幺逆(凤姐要你)
实在不好理解的话,可以把群类比成一个魔方,魔方的旋转就是运算,得到的运算结果(集合中的元素们)就是旋转魔方后,魔方上面整体的颜色分布。
魔方一共就那些颜色排列组合,把所有魔方颜色分布的排列组合集合起来,就是整个集合,在满足 “旋转” 这个运算的前提下,这些集合就构成群(因为如果你选择把魔方拆开这个运算,那得到的一定是散成一片的方块,该状态就不在上述魔方例子的集合内)
易得,旋转矩阵集合和矩阵乘法构成群,后面要介绍的变换矩阵
SE(n)和矩阵乘法也构成群。正因为如此,才能称他们为旋转矩阵群和变换矩阵群。李群是指具有连续(光滑)性质的群。
像整数群$\left \langle \mathbb Z,+ \right \rangle $就是离散的,并不是李群。
像SO(n),SE(n),在实数空间上是连续的,我们可以稍微想象一下,一个刚体在空间中连续的旋转,所以这种算是李群。
关于李群李代数,在本篇中就不展开介绍了,后续再详细介绍。
根据上面的补充资料,我们可以知道,SO(n)是由n维空间的旋转矩阵组成,所以说,SO(3)就是特指三维空间了。通过这个旋转矩阵,我们可以直接讨论两个坐标系之间的旋转变换了。
因为旋转矩阵是正交矩阵,那他的逆就描述了一个相反的旋转。
$$
a^{\backprime}=R^{-1}a=R^{T}a
$$
在欧式变换中,除了刚刚咱讨论的旋转,还有平移。把旋转和平移合在一起,就可以用公式:
$$
a^{\backprime}=Ra+t
$$
t自然就是指平移向量了。相比前面旋转的部分,平移只需要直接把平移向量加上去就好了,看上去非常简单。在实际应用中,我们会定义坐标系1,坐标系2,那么向量a在两个坐标系下的坐标a1,a2的关系如下:
$$
a_{1}=R_{12}a_{2}+t_{12}
$$
这里R12是指把坐标系2的向量变换到坐标系1,因为向量乘在这个矩阵的右边,下标要从右往左读的。
对于平移t12,虽然确实是指从1到2的向量,但要注意,反过来的t21并不等于-t12,这两个向量的坐标值并不是相反数。
3、变换矩阵与齐次坐标
就上面我们讨论过的式子来说,虽然可以完美表达欧式空间的旋转与平移,不过还有一个问题:这里的变换并不是一个线性关系
假设我们进行2次变换:R1、t1与R2、t2
$$
b=R_{1}a+t_{1},c=R_{2}b+t_{2}
$$
那,从a到c的变换就是:
$$
c=R_{2}(R_{1}a+t)+t_{2}
$$
这样的形式面对实际应用中多次的变换,会显得很繁琐。所以引入了齐次坐标和变换矩阵,重写的式子如下:
$$
\begin{bmatrix}
a^{\backprime}\\
1
\end{bmatrix}=
\begin{bmatrix}
R & t\\
0^{T} & 1
\end{bmatrix}
\begin{bmatrix}
a\\
1
\end{bmatrix}
\overset{\mathrm{def}}{=}
T\begin{bmatrix}
a\\
1
\end{bmatrix}
$$
我们在三维向量的末尾添加1,让他变成四维向量,称之为齐次坐标。对于这个四维向量,我们可以把旋转和平移写在一个矩阵里,使得整个关系变成线性关系。我们把式子末尾大写T称之为变换矩阵。
如果我们暂时使用$\overset{\sim }{a}$表示为a的齐次坐标,那对于该标题头两次变换的例子来说,可以写成如下式子:
$$
\overset{\sim }{b}=T_{1}\overset{\sim }{a},\overset{\sim }{c}=T_{2}\overset{\sim }{b} \rightarrow \overset{\sim }{c}=T_{2}T_{1}\overset{\sim }{a}
$$
在不引起歧义的前提下,我们可以适(tou)当(lan)简写成$b=Ta$的样子,默认里面已经进行了其次坐标变换
需要注意的是,不进行齐次坐标变换的时候,这边的乘法在矩阵维度上是不成立的
这个变换矩阵T很有意思:左上角是旋转矩阵,右上角是平移向量,左下角是0向量,右下角是1。这种矩阵又称为特殊欧氏群
$$
SE(3)=\left \{ T=
\begin{bmatrix}
R & t\\
0^{T} & 1
\end{bmatrix}
\in \mathbb R^{4 \times 4} |
R\in SO(3),t\in \mathbb R^{3}
\right \}
$$
和那个SO(3),一样,该矩阵的逆就表示一个反向的变换:
$$
T^{-1}=
\begin{bmatrix}
R^{T} & -R^{T}t\\
0^{T} & 1
\end{bmatrix}
$$
我们也用$T_{12}$的写法来表示从2到1的变换。
4、旋转向量
有了旋转向量来描述旋转,有了变换矩阵描述一个6自由度的三维刚体运动,但是聪明的你一定注意到了,上面这种矩阵的方式至少有这两个缺点:
- SO(3)的旋转矩阵有9个量,但一次旋转就只有三个自由度,这种表达方式有点冗余
- 旋转矩阵必须是正交矩阵,且行列式为1!变换矩阵也是这样。如果想估计或者优化一个旋转矩阵、变换矩阵的时候,这些约束对于邱洁问题来说会变得更加困难。
所以,我们希望有一种方式可以紧凑地描述旋转平移,比如就用一个六维的向量来表示变换,有没有这样一种方式呢?
事实上,任意旋转都可以用一个旋转轴和一个旋转角来描述。咱用一个向量,方向和旋转轴一致,长度等同于旋转角,这种向量我们叫它旋转向量
同样的,对于变换矩阵来说,我们用一个旋转向量加平移向量就可以表达一次变换了,这时的变换维度正好是六维。
设旋转轴为一个单位长度的向量n,角度θ,那向量θn也可以描述这个旋转,那旋转矩阵和旋转向量之间有一个什么联系呢?
从旋转向量到旋转矩阵只需要用罗德里格斯公式就可以了。
罗德里格斯公式的推导如下:

假设v在三维空间中,绕单位旋转轴 k(我们后面用f表示这个轴),旋转θ。
从上图可以看出,对于向量v可以分出两个分向量: v平行和v垂直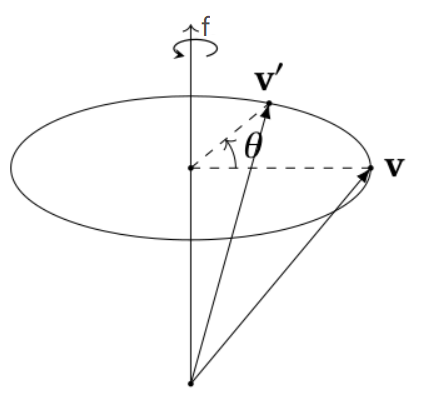
从上图可看到,v 向量旋转了 θ 角到 v’ 向量,我们要求的是这个旋转后的 v‘ 向量,这个可以用f,v,theta表示出来
其中需要说明的是,f的完整形式应该是$[f_x,f_y,f_z]^T$。如果算上一个绕着的θ,这样就有四个变量(自由度)了。
但是像欧拉角,其实就三个变量(自由度)。 为了消除旋转轴 f 模长这个多余的自由度 , 我们可以规定旋转轴 f 的模长为
$$
\parallel f \parallel =\sqrt{f_x^2+f_y^2+f_z^2}=1
$$
因为限定了模长已知,这样就可以知道其中两个变量 f 去求第三个变量了。 也可以说 f 是一个单位向量。,后面推导更方便我们把v向量正交分解开来,就有一个v平行和一个v垂直向量。v平行就是在f上的投影向量。
这个v平行可以写成如下形式:
$$
v_{||} =\frac{f \cdot v}{f \cdot f}f=\frac{f\cdot v}{\parallel f \parallel ^{2}}f=(f\cdot v)f
$$
其中,分子是f和v的点积相乘,分母就是f的模长,然后后面乘一个f,相当于乘了向量的方向。因为模长是1,所以最后可以化简为:f点积v乘一个f因为根据向量的运算,$v=v_{||}+v_{\bot }$,所以$v_{\bot }=v-v{||}$。展开可得:
$$
v{\bot}=v-(f\cdot v)f
$$
绕着v平行旋转的话,因为v平行和f轴平行,所以旋转后和旋转前都一样。v平行’ = v平行。v⊥正交于f 的 ,这个旋转可以看做是平面内的旋转。因为旋转不改变 v ⊥ 的长度,所以路径是一个圆。 下面是这个旋转的示意图,右侧的为俯视图。
由于在这个平面上我们只有一个向量 v ⊥ ,用它来表示一个旋转是不够的,我们还需要构造一个同时正交于 u和 v 的向量 w,这个可以通过叉乘来获得:$w=f \times v\bot$
$$
\parallel w \parallel = \parallel f\times v_{\bot} \parallel
=\parallel f \parallel \times \parallel v_{\bot} \parallel \times sin\frac{\pi }{2}=\parallel v_{\bot} \parallel
$$
因为夹角是f和v⊥的夹角,因为这俩是正交的,显然角度是$\frac{\pi }{2}$。也就是说,w 和 v⊥ 的模长是相同的,所以,w 也位于圆上。
有了这个新的向量 w,就相当于我们在平面内有了两个坐标轴。我们现在可以把 v ′ ⊥ 投影到 w 和 v ⊥ 上,将其分解为$v_{v}^{\backprime}$和$v_{w}^{\backprime}$。那就是$v_{\bot}^{\backprime}=v_{v}^{\backprime}+v_{w}^{\backprime}$。使用一点三角的知识我们就能得到:
$$
v_{\bot}^{\backprime}=\cos{\theta}\cdot v_{\bot}+\sin{\theta}\cdot w=\cos{\theta}\cdot v_{\bot}+\sin{\theta}\cdot(f\times v\bot)
$$
将上面两个结果加起来,就是:
$$
v^{\backprime}=v_{\parallel}^{\backprime}+v_{\bot}^{\backprime}=v_{\parallel}^{\backprime}+\cos{\theta}\cdot v_{\bot}+\sin{\theta}\cdot(f\times v\bot)
$$
因为我们前面说过:
$$
v_{\parallel}=(f\cdot v)f,v{\bot}=v-(f\cdot v)f
$$
然后 f 轴又和 v平行 平行,叉乘得0,可得:
$$
f\times v_{\bot}=f\times (v-v_{\parallel})=f\times v+f\times v_{\parallel}=f\times v-0
$$
最终可得:
$$
v^{\backprime}=(f\cdot v)f+\cos{\theta}(v-(f\cdot v)\cdot f)+\sin{\theta}(f\times v)
$$
化简一下:
$$
v^{\backprime}=\cos{\theta}v+(1-\cos{\theta})(f\cdot v)\cdot f+\sin{\theta}(f\times v)
$$
至此,公式推导完毕
但扯皮这么长的公式,我们得代数进来。需要参考前面讲过的公式了。
$$
Rv=\cos{\theta}v+(1-\cos{\theta})(f\cdot v)\cdot f+\sin{\theta}(f^{\wedge}v)
$$因为 (v·f)·f = f·(v·f) , 然后由于v·f = fT·v ,所以原式转化为f·fT·v
所以可得:
$$
Rv=\cos{\theta}v+(1-\cos{\theta})(f^{T}f)v+\sin{\theta}(f^{\wedge}v)
$$
化简可得:
$$
R=\cos{\theta}I+(1-\cos{\theta})(f^{T}f)+\sin{\theta}(f^{\wedge})
$$
对于转角theta,取两边的迹:
$$
tr\left (R\right )=\cos{\theta}tr(I)+(1-\cos{\theta})tr(f^{T}f)+\sin{\theta}tr(f^{\wedge})=3\cos\theta+(1-\cos\theta)=1+2\cos\theta
$$
因此:
$$
\theta=\arccos\frac{tr\left(R\right)-1}{2}
$$
关于转换公式,还可以自行了解李代数,可以发现它们和SO(3)上李群与李代数之间的对应关系。
5、欧拉角
欧拉角就不太展开介绍了,就是三个分离的转角,把一个旋转分解成3次让不同轴的旋转。长相如下。
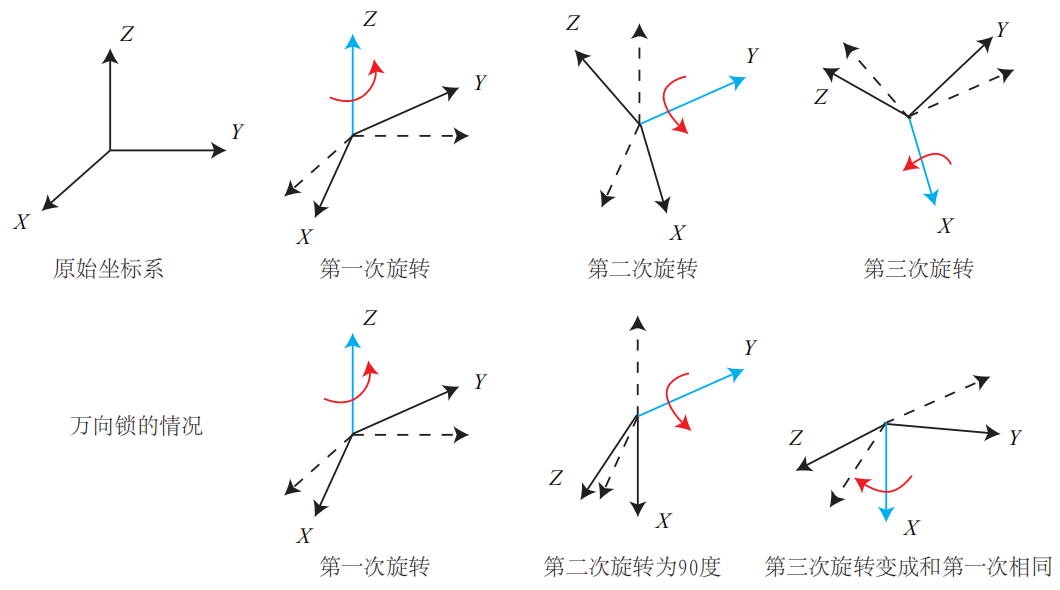
上图介绍的是欧拉角的一个重大的缺点:万向锁问题。万向锁问题会导致第三次旋转和第一次旋转的效果相同。
如果上图不好理解的话,可以参考这个动图。可以看到,蓝色轴和绿色轴叠在一起的时候,不管移动绿轴还是蓝轴,都只是在同个方向上转动,直接丢失了一个自由度,形成万向锁。

由于这种奇异性问题[1],欧拉角不适用于插值、迭代,往往只适合用于人机交互,这里需要引出我们真正需要使用的:
6、四元数
旋转矩阵用9个量描述3个自由度的旋转,具有冗余性;
欧拉角和旋转向量是紧凑的,但具有奇异性。
事实上,我们是找不到不带奇异性的三维向量描述方式的。
希望既能保持紧凑性,又能没有奇异性,就需要使用四元数。
四元数可以类比复数,例如说,我们想将复平面的向量旋转90度,可以给这个复向量乘以$e^{i\theta}$。当他转化为普通形式就是$e^{i\theta}=\cos\theta+i\sin\theta$。
所以在二维中,旋转可以用单位复数描述。类似,在三维中,我们就使用四元数来描述:
$$
q = q_{0}+q_{1}i+q_{2}j+q_{3}k
$$
其中,i、j、k是四元数的三个虚部,满足以下关系:
$$
\left\{\begin{matrix}
i^{2}=j^{2}=k^{2}=-1 \\
ij=k;ji=-k \\
jk=i;kj=-i \\
ki=j;ik=-j
\end{matrix}\right.
$$
如果把ijk看成三个坐标轴,那他们与自己的乘法和复数的乘法一样,相互之间的乘法和外积一样。有时人们也用一个标量和一个向量来表示四元数:
$$
q=[s,v]^{T},s=q_{0}\in\mathbb R,v=[q_1,q_2,q_3]^{T}\in\mathbb R^3
$$
s是四元数的实部,v是四元数的虚部。如果一个四元数的虚部为0,则称为实四元数;如果实部为0,就是虚四元数。
6.1 四元数运算
四元数和通常的复数一样,可以进行各种运算。比如四则运算、共轭、求逆、数乘等等。
设两个四元数$q_a,q_b$,向量$[s_a,v_a],[s_b,v_b]$,或者$q_a=s_a+x_{a}i+y_{a}j+z{a}k$,$q_b=s_b+x_{b}i+y_{b}j+z{b}k$。
6.1.1加减法
$$
q_a\pm q_b=[s_a\pm s_b,v_a\pm v_b]
$$
6.1.2 乘法
把qa的每一项和qb的每一项相乘,最后相加。虚部要按照i、j、k三个虚部的运算关系进行:
$$
q_{a}q_{b}=s_as_b-x_ax_b-y_ay_b-z_az_b\\
+(s_ax_b+x_as_b+y_az_b-z_ay_b)i\\
+(s_ay_b-x_az_b+y_as_b+z_ax_b)j\\
+(s_az_b+x_ay_b-y_ax_b+z_as_b)k
$$
如果写成向量形式并利用内外积运算,会有更加简洁的表达式:
$$
q_aq_b=[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a\times v_b]^{T}
$$
在这种乘法定义下,俩实四元数乘积和复数一样,仍然是实的。But,由于最后一项外积的存在,四元数乘法通常是不可以交换的,除非$v_a,v_b$在$\mathbb R^3$中共线,外积项变成0,就可以进行乘法交换。
6.1.3 模长
两个四元数的模就是模的乘积。(所以单位四元数相乘之后仍然是四元数)
$$
\parallel q_a \parallel =\sqrt{s_a^2+x_a^2+y_a^2+z_a^2}\\
\parallel q_aq_b \parallel = \parallel q_a \parallel \parallel q_b \parallel
$$
6.1.4 共轭
四元数共轭和本身相乘,会得到一个实四元数,其实部为模长的平方。
$$
q_a^{*}=s_a-x_{a}i-y_{a}j-z_{a}k=[s_a,-v_a]^T\\
q^{*}q=qq^{*}=[s_a^2+v^Tv,0]^T
$$
6.1.5 逆
一个四元数的逆是:
$$
q^{-1}=q^*/\parallel q \parallel^2
$$
按照这个定义,四元数和自己的逆的乘积为实四元数1:
$$
qq^{-1}=q^{-1}q=1
$$
若q是单位四元数,它的逆和共轭就是同一个量。同时,乘积的逆具有和矩阵相似的性质:
$$
(q_aq_b)^{-1}=q_b^{-1}q_a^{-1}
$$
6.1.6 数乘
和向量类似,四元数可以与数相乘
$$
kq=[ks,kv]^T
$$
6.2 四元数表示旋转
我们可以使用四元数表达对一个点的旋转。
假设说,有一个点$p=\left [ x,y,z \right ]\in\mathbb R^3$,以及一个由单位四元数q指定的旋转。三维点p经过旋转之后变成p‘,用矩阵的方式描述的话,就是p’=Rp。
用四元数的方式描述,就是:
$$
p=[0,x,y,z]^T=[0,v]^T
$$
相当于把四元数的三个虚部和空间中的3个轴对应。旋转后点p’可以这样表示乘积:
$$
p^{‘}=qpq^{-1}
$$
这里的乘法就是四元数乘法,得到的结果也将是四元数。计算结果的实部为0,所以是纯虚四元数。
6.3 四元数到其他旋转表示的转换
设$q=\left [ s,v \right ]^T $,以下来讨论四元数与旋转向量、旋转矩阵的关系。首先,定义如下的符号:
$$
q^+=
\begin{bmatrix}
s & -v^T\\
v & sI+v^{\wedge }
\end{bmatrix},
q^{\oplus}=
\begin{bmatrix}
s & -v^T\\
v & sI-v^{\wedge }
\end{bmatrix}
$$
这两个符号把四元数映射成一个4x4的矩阵。
$$
q_1^+q_2=
\begin{bmatrix}
s & -v^T\\
v & sI+v^{\wedge }
\end{bmatrix}
\begin{bmatrix}
s_2\\
v_2
\end{bmatrix}=
\begin{bmatrix}
-v_1^Tv_2 + s_1s_2\\
s_1v_2+s_2v_1+v_1^{\wedge}v_2
\end{bmatrix}=
q_1q_2
$$
同理,我们可以证得:
$$
q_1q_2=q_1^+q_2=q_2^{\oplus}q_1
$$
我们考虑到用四元数对空间点进行旋转的问题。参考前面的说法,我们代入上面式子可得:
$$
p^{‘}=qpq^{-1}\\
=q^+p^+q^{-1}\\
=q^+q^{-1}p
$$
然后代入两个符号对应的矩阵:
$$
q^+(q^{-1})^{\oplus}=
\begin{bmatrix}
s & -v^T\\
v & sI+v^{\wedge }
\end{bmatrix}
\begin{bmatrix}
s & v^T\\
-v & sI+v^{\wedge }
\end{bmatrix}=
\begin{bmatrix}
1 & 0\\
0 & vv^T+s^2I+2sv^{\wedge}+(v^{\wedge})^2
\end{bmatrix}(*)
$$
因为 p’ 和 p 都是虚四元数,所以事实上,该矩阵右下角就是给出了从四元数到旋转矩阵的变换关系
$$
R=vv^T+s^2I+2sv^{\wedge}+(v^{\wedge})^2
$$
然后我们不是还有旋转向量嘛
为了得到四元数到旋转向量的转换公式,我们对式子左右两边求迹:
$$
tr\left (R\right)=tr(vv^T)+3s^2+2s\cdot 0+tr((v^{\wedge})^2)\\
=v_1^2+v_2^2+v_3^2+3s^2-2(v_1^2+v_2^2+v_3^2)\\
=(1-s^2)+3s^2-2(1-s^2)\\
=4s^2-1
$$
因为我们前面计算旋转向量的时候,得到过一个式子,把它代进去:
$$
\theta = \arccos(\frac{tr \left (R \right )-1}{2})=\arccos(2s^2-1)
$$
可得:
$$
\cos\theta=2s^2-1=2\cos^2\frac{\theta}{2}-1
$$
所以:
$$
\theta = 2\arccos s
$$
关于旋转轴,在上面式子(*)中,用q的虚部代替p,就可以知道,q的虚部组成的向量在旋转时是不动的,就构成了旋转轴,所以只要除掉他的模长就可以得出。
所以,四元数到旋转向量的转换总结如下:
$$
\left\{\begin{matrix}
\theta = 2\arccos q_0 \\
\left [ n_x,n_y,n_z \right ]^T=\frac{\left [ q_1,q_2,q_3 \right ]^T}{\sin\frac{\theta}{2}}
\end{matrix}\right.
$$
6.4 相似、仿射、射影变换
处理欧式变换之外,三维空间中还有很多种变换方式
只是欧式变换最简单,他保持了向量的长度与夹角,相当于说,我们把一个刚体原封不动地进行移动旋转。
其他的变换方式则是会改变其外形。
他们都拥有类似的矩阵表示。
1、相似变换
比欧式变换多了一个自由度,允许物体进行均匀缩放:
$$
T_s=
\begin{bmatrix}
sR & t\\
0^T & 1
\end{bmatrix}
$$
不难看出,旋转部分多了一个缩放因子s,表示对其向量旋转之后,可以在x,y,z坐标上进行均匀缩放。
可以想象一下,一个边长为1的正方体缩放成边长为10的正方体,差不多是这么个效果。
三维相似变换的集合也叫做相似变换群,记做Sim(3)。
2、仿射变换
$$
T_a=
\begin{bmatrix}
A & t\\
0^T & 1
\end{bmatrix}
$$
和欧式变换的区别是:方式变换只要求A是一个可逆矩阵,而没必要是正交矩阵。
仿射变换,也叫做正交投影
一个立方体,经过仿射变换之后,立方体就不再是正方的了,但各个面仍然是平行四边形。
3、射影变换
$$
T_p=
\begin{bmatrix}
A & t\\
a^T & v
\end{bmatrix}
$$
左下角元素为缩放。由于用了齐次坐标,v≠0时,我们可以对整个矩阵除以v得到一个右下角为1的矩阵,否则右下角为0。
2维的射影变换有8个自由度,3维的有15个自由度。
射影变换是现在讲的过程中,形式最一般的。
可以类比为:从真实世界到相机照片的变换。
可以想象一下,在相机中拍的正方形可能都不会是正方形了,由于视角以及近大远小,你有时可以拍出不规则的四边形。
| 变换名称 | 自由度 | 不变的性质 |
|---|---|---|
| 欧式变换 | 6 | 长度、夹角、体积 |
| 相似变换 | 7 | 体积比 |
| 仿射变换 | 12 | 平行性、体积比 |
| 射影变换 | 15 | 接触平面的相交与相切 |






